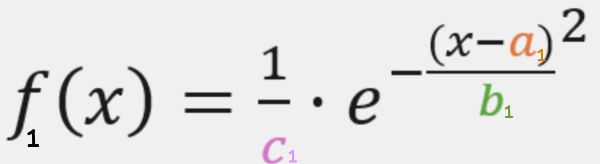
Annäherung an eine Binomialverteilung
Wir haben bereits herausgefunden, welchen Einfluss die Parameter auf den Graphen der e-Funktion haben. Jetzt wollen wir dieses Wissen nutzen, um den Graphen an ein Histogramm der Binomialverteilung anzunähern.
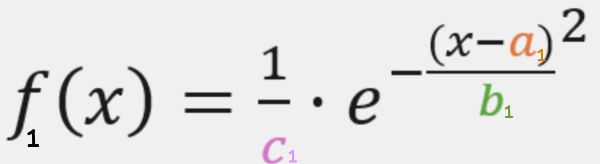
1. Annäherung
[size=150]Im Applet 1 sehen Sie das Histogramm einer Binomial-Verteilung für einen Stichprobenumfang von n=50 und einer Trefferwahrscheinlichkeit von p=0,4. [/size]
Aufgabe:
[list=1][size=150][*]Verschieben Sie die Schieberegler im Applet 2 und bestimmen Sie die Parameter a,b und c so, dass der Graph der e-Funktion möglichst die Mittelpunkte der oberen Kante der Säulen verbindet.[/*][*]Machen Sie einen Screenshot von Ihrer angenäherten Kurve und fügen Sie diesen in Ihre Notizen ein.[/*][/size][/list]
Applet 1: Histogramm einer binomialverteilten Zufallsgröße mit n=50, p=0,4
2. Annäherung
[size=100]Wir verändern noch ein Mal unsere Funktion:[br][br][/size]
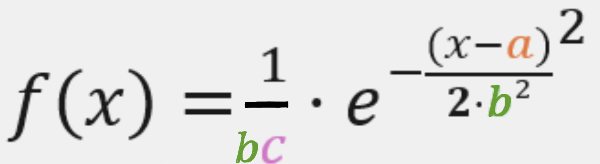
[size=200][size=100][size=150]Unten im Applet 2 sehen Sie das Histogramm einer Binomialverteilung mit n = 30 und p = 0,3. Berechnen Sie den Erwartungswert und die Standardabweichung. Geben Sie Ihre Ergebnisse ein.[/size][/size][/size]
Erwartungswert:
Standardabweichung:
Aufgabe
[size=150]Verschieben Sie die Schieberegler im Applet 2 und estimmen Sie die Parameter a und b so, dass der Graph der e-Funktion möglichst die Mittelpunkte der oberen Kante der Säulen verbindet. [br]Machen Sie ein Screenshot für Ihre Notizen.[/size]
Αpplet 2: Histogramm einer binomialverteilten Zufallsgröße mit n=30, p=0,3
Der Zusammenhang zwischen den Kenngrößen und der Funktionsgleichung
Beschreiben Sie den Zusammenhang zwischen unserer Funktiongleichung und den berechneten Kenngrößen des Erwartungswertes und der Standardabweichung.
Wie kommt es zu den Parameter c?
Die Funktion, die wir suchen, soll eine Wahrscheinlichkeitsdichte werden. [br]Das heißt es müssen folgende Bedingungen gelten:[br]1) [math]f\left(x\right)\ge0[/math] für alle x aus unserem Intervall und[br]2) [math]\int_a^bf\left(x\right)dx=1[/math].
Begründen Sie, dass die erste Bedingung für eine Wahrscheinlichkeitsdichte bereits erfüllt ist.
In dem Applet 3 wird näherungsweise die Fläche unter dem Graphen berechnet. Das Ergebniss wird bei d angegeben. Warum handelt es sich hier noch nicht um eine Wahrscheinlichkeitsdichte?[br]
Applet 3: Fläche unter dem Graphen
Verschieben Sie den Schieberegler c so, dass die zweite Bedingung für eine Wahrscheinlichkeitsdichte erfüllt ist. [br]Geben Sie an welchen Wert c näherungsweise annehmen muss.
Verschieben Sie nun die Schieberegler für a und b im Applet 3. Was muss nun für c gelten, damit f weiterhin eine Wahrscheinlichkeitsdichte bleibt? Wählen Sie die richtige(n) Antwort(en) aus.