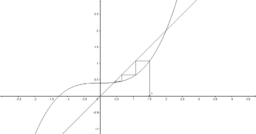
The equation [math]f(x)=0[/math] can be solved with fixed point iteration by rearranging into the form [math]x=g(x)[/math] and calculating successive iterates from that. When students first see this method there seems to be no obvious pattern about which rearrangements or starting values will converge to a solution.
Fixed point iteration can be shown graphically, with the solution to the equation being the intersection of [math]y=x[/math] and [math]y=g(x)[/math]. The resulting patterns show convergence or divergence (and described as 'staircase' or 'cobweb', depending on the shape).
Leave [math]f(x)=x[/math] and change [math]g(x)[/math] in the window to suit the equation you are solving.
(This is a work in progress; I'll update the user interface to this when I get time).