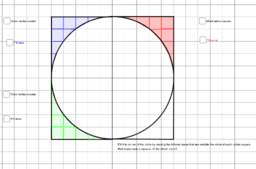
Step 1: Draw 1 of the radius squares. Discuss how this square is created by the radius of the circle, which is 5 units. Discuss the area of this square. (It is a 5 by 5 square, so students should be able to articulate that it is 5 squared, or 25 square units.)
Step 2: Draw the other radius squares. Discuss the area of the entire square that the circle is inscribed in (100 square units). We can estimate that the area of the circle will be less than 100 square units.
Step 3: Estimate the area of one of the quarters of the circle by counting the square units. Encourage students to put together partial squares, if needed. They should be able to estimate somewhere between 18-20 square units.
Step 4: Fill the area of the quarter that you've estimated to check how close students got. What can you assume about the other quarters?
Step 5: We're going to compare how many radius squares will fill the entire circle to see the relationship between the radius and it's area. Starting with the red section, begin moving the pieces that are not inside the circle to the white section of the circle. Make sure you're filling INSIDE the circle, since that's the area we are looking for. Continue to fill the white section with the blue outer pieces and the green outer pieces.
Step 6: Did we fill the area of the entire circle? (No) Did we get close? (Yes) How close- that is, how many radius squares would we need to fill the area? (I always say "3 and a little bit more of those radius squares would fill the entire circle" which is where 3.14r^2 comes from.)