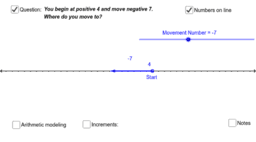
Integers can sit to the left or right of zero on the number line. If they are negative, they sit to the left. If they are positive, they sit to the right. Integers can also make a movement. A movement to the left makes a negative number. A movement to the right makes a positive number. Because integers are sometimes negative, you will notice patterns in how integers add that look different from the patterns for how whole numbers add. This applet will help you explore patterns in how addition works.
This applet will help you explore patterns for how addition works. It shows addition as the outcome of a movement from the open dot by a movement from that dot. It does not matter where that dot sits or which way the movement goes. The dot can sit on either side of zero, the movement can go toward or away from zero, or it can go to the left or to the right. Regardless of where the dot sits or which way the movement goes, the result for addition is always the new position at which you arrive. So, you only need to think of the operation of addition in one way.
Use the dynamic diagram to figure out how addition really works. After a while, test your understanding by figuring out answers without the diagram.
The applet treats all numbers as integers. It may be used in several ways. First, it may be used as a prompt for interviewing students about how they deal with the addition of integers. Used in this way you would probably want to select only the question and the diagram. As a tool for concerted instruction you can either have students calculate sums by means of the diagram or by means of a symbolic and/or "wordy" description of the the addition process.