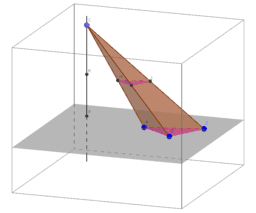
Sezioni delle piramidi
Si dimostra che due sezioni parallele di una piramide sono poligoni simili e che
il rapporto delle loro aree è uguale al rapporto delle altezze al quadrato.
Illustrazione con GeoGebra 3 dimensioni.
Si disegni un poligono qualunque nella Vista Grafica
Si apra la Vista grafici 3d con Visualizza -> Grafici 3d. Il poligono appare
disegnato nel piano con z=0
Il punto di vertice della piramide potrebbe muoversi su di un piano parallelo alla base.
Prendiamo un punto D di coordinate (0,0,5). Per fare ciò, nella riga di inserimento basta
scrivere D=(0,0,5). Ovviamente invece di 5 si può scegliere un altro numero.
A questo punto disegnamo il piano su cui si troverà il vertice con Piano -> Piano Parallelo
clic sul punto D e sul piano di base.
Utilizzare adesso Punto -> Punto su oggetto per avere un punto E sul piano appena disegnato.
Verificare con il Muovi che E si muove sul piano
Disegnamo la piramide indicando il poligono di base e il vertice E
Disegnamo la retta passante per il vertice E e pependicolare al piano di base.
Con il bottone intersezione troviamo il punto F intersezione fra retta e piano di base.
Per disegnare un piano che si sposta parallelo alla base della piramide partiamo dal
definire un cursore o slider numerico fra 0 e 5 incremento 0.1 di nome h.
Questo ci permette di definire un punto mobile G=(0,0,h) e quindi come prima un piano
passante per G e parallelo al piano di base della piramide di nome g. verificare con il Muovi
il fatto che il piano g si sposta al variare di h.
Indichiamo con K il punto di intersezione fra la retta passante per E e perpendicolare
al piano di base e il piano "mobile" g.
Con lo strumento Interseca due superfici, possiamo individuare le sezioni della piramide
e colorarle in modo che risultino più evidenti; è anche possibile nascondere i due piani paralleli
e gli assi cartesiani.
L'altezza relativa alla base della piramide sarà EF, quella relativa alla sezione EK.
Definiamo quindi EF ed EK come due segmenti.
A questo punto è facile verificare quanto detto all'inizio dato che le aree delle sezioni
e le lunghezze dei segmenti compaiono nella vista algebra: si calcola il rapporto delle aree
e il rapporto dei quadrati delle altezze. Al variare di h questi rapporti risultani costantemente
uguali.