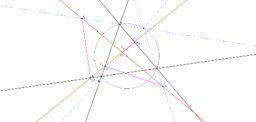
A nice generalization of the Simson line theorem
Problem 1:
Let ABC be a triangle, let a line L through circumecenter, let a point P lie on circumcircle. Let AP,BP,CP meets L at A_P, B_P, C_P.
Denote A_0,B_0,C_0 are projection (mean perpendicular foot) of A_P, B_P, C_P to BC,CA,AB respectively. Then A_0,B_0,C_0 are collinear.
- When (l) pass through P, this line is Simson line.
Problem 2: The new line \overline {A_0B_0C_0} bisect the orthocenter and P