Curvas de Lissajous (Upgrade)
Projeto: Rumo à Evolução
Animações feitas no software livre de geometria dinâmica com o objetivo de valorizar os principais recursos das construções geométricas. A ideia original é apresentar um passo a passo explicando cada um dos comandos utilizados por meio de um livro do tipo "Faça você mesmo".
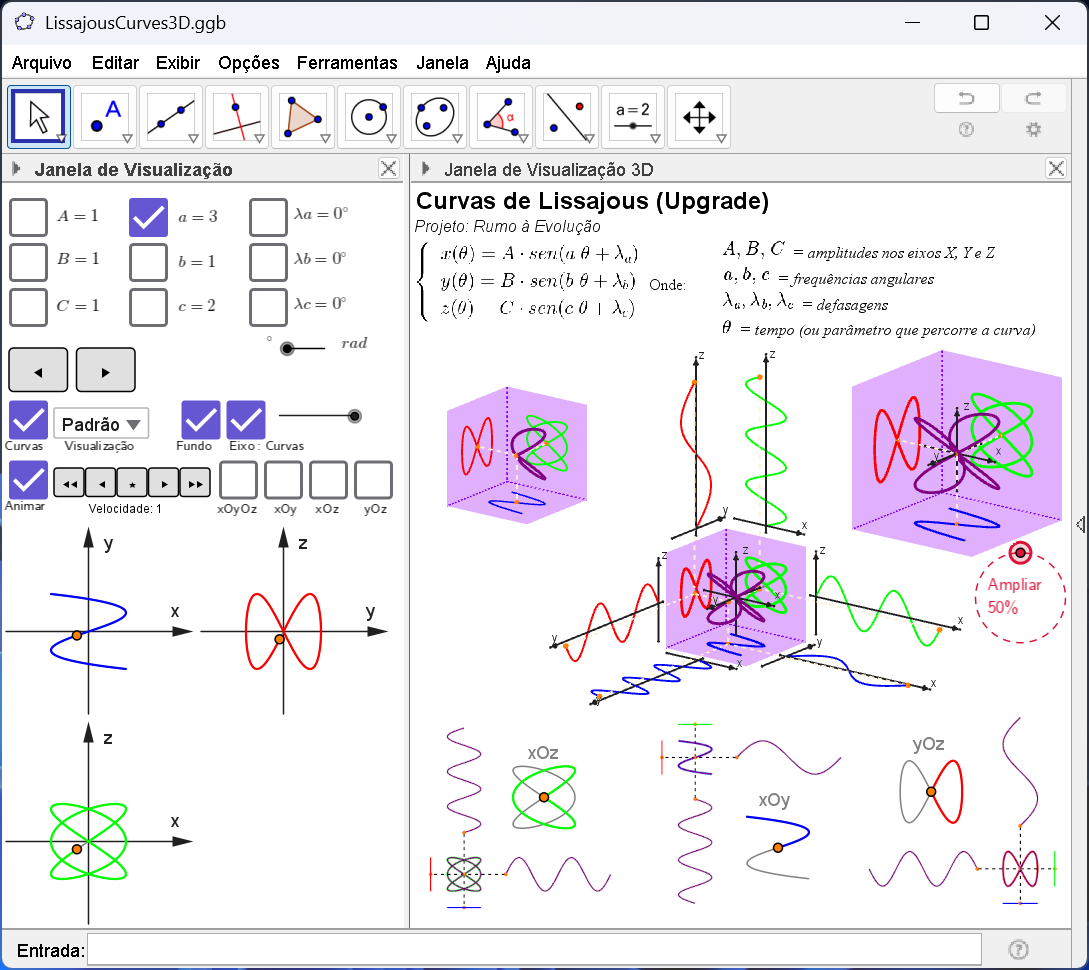
No projeto "Rumo à Evolução", semelhante a aplicação Curvas de Lissajous (Lissajous Curves) em que apresentamos figuras geométricas traçadas por um ponto que se move de acordo com duas oscilações harmônicas perpendiculares entre si. Nessa aplicação, temos as equações paramétricas: x(θ) = A sen(a θ + λa), y(θ) = B sen(b θ + λb) e z(θ) = C sen(c θ + λc) onde θ é o parâmetro que percorre a curva; A, B e C são amplitudes nos eixos X, Y e Z; a, b e c são frequências angulares; e λa, λb e λc são defasagens entre as oscilações pode ser definidos em graus ou radianos.
Dessa forma, definido os parâmetros da curva, na janela de visualização 2D (J2D) temos individualmente os eixos xOy, xOz, yOz e na janela de visualização 3D (J3D) a projeção dessa curva tridimensional. Caso necessário, é possível exibir os planos (opção Fundo), os Eixos (opção Eixo) e temos a opção Ampliar, em que aumentamos em até 200% a curva tridimensional para uma melhor visualização.
Além disso, temos a opção de explorar individualmente o passo a passo das construção da Curvas de Lissajous sobre o plano 3D e as curvas sobre os planos XY, XZ e YZ. Para isso, selecionamos a opção: xOyOz, xOy, xOz e yOz, respectivamente. Na opção tipo de visualização do plano, temos "Padrão" (Plano 3D), "Plano XY", "Plano XZ" e "Plano YZ" e na opção animar, acompanhamos o traçado completo de cada curva podendo modificar a velocidade da execução do traçado.
Finalmente, selecionando a opção Curvas, o efeito da opção Ampliar é anulada porque não só exploramos individualmente o passo a passo das construção da Curvas sobre o plano 3D ou sobre os planos XY, XZ e YZ, também visualizamos a curvas sobre os eixos xOy, xOz e yOz a medida que variamos o parâmetro θ, podendo ser individualizado quando selecionado a opção tipo de visualização do plano.
Enquanto o livro não está disponível, curta a página "Gifs Animados de Construções Geométricas" em http://www.facebook.com.br/almeidacrm/" e não seja o último a saber das novidades ainda não compartilhadas.