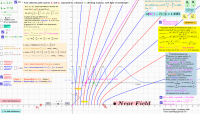
Curves of constructive and destructive interference from two point sources in the "near" and "far" fields

The resulting hyperbolic interference lines are modeled mathematically using the distance b between the sources and the wavelength λ of the radiation. It takes into account the principle that the path difference Δ must be less than the distance b between the sources. If Δ≥b, the triangle inequality would be violated, making it physically impossible to find a point that satisfies this condition and therefore rendering interference impossible. It is shown that in the limiting transition (from near to far field), the hyperbolas of the interference pattern transform into straight lines: y=x*sqrt((b/(r*λ))2-1), where r takes on integer and half-integer values. These lines correspond to the far-field approximation, in which the path difference is given by Δ=b* sin(θ).