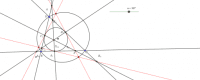
Let ABC be a triangle, P=X(13) or X(14) let three line d1, d2, d3 through P such that angle of them: angle(d1, d2)=angle(d2,d3)=pi/3. Let d1 meets BC, CA, AB at A1, B1, C1; d2 meets BC, CA, AB at A2, B2, C2; d3 meets BC, CA, AB at A3, B3, C3. Then A1, B2, C3 are collinear (named of this line l1); A2, B3, C1 are collinear (named of this line l2); A3, B1, C2 are collinear (named of this line l3). Then triangle formed by l1, l2, l3 are DEF then A, B, C, D, E, F lie on a circumconic (of ABC) and AB, BC, CA, DE, EF, FD tangent to a inconic (of ABC).