[b]Funciones trigonométricas inversas[/b]
Las funciones trigonométricas son todas funciones periódicas. Así las gráficas de ninguna de ellas pasa la prueba de la línea horizontal y tampoco son 1-a-1. Esto significa que ninguna de ellas tiene una inversa a menos que el dominio de cada una esté restringido a hacer de ella una 1-a-1.
Ya que las gráficas son periódicas, si escogemos un dominio adecuado podemos usar todos los valores del rango.
Si restringimos el dominio de f(x) = sin x a hemos hecho la función 1-a-1. El rango es [–1, 1].
(Aunque hay muchas formas de restringir el dominio para obtener una función 1-a-1 esto es de acuerdo con el intervalo usado.)
Denotamos la función inversa como y = sin–1x. Se lee y es la inversa del seno de x y significa que y es el ángulo de número real cuyo valor de seno es x. Pero tenga cuidado con la notación usada. El superíndice “–1” NO es un exponente. Para evitar esta notación, algunos libros usan y = arcsin x como notación.
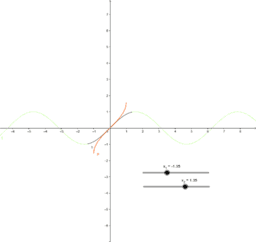
Para graficar la inversa de la función seno, recuerde que la gráfica es una reflexión sobre la recta y = x de la función seno.
Dese cuenta que el dominio es ahora el rango y el rango es ahora el dominio. Ya que el dominio está restringido a todos los valores positivos nos arrojará un ángulo de