Brincando com Torus - Um pouquinho mais ...
Projeto: Rumo à Evolução
Animações feitas no software livre de geometria dinâmica com o objetivo de valorizar os principais recursos das construções geométricas. A ideia original é apresentar um passo a passo explicando cada um dos comandos utilizados por meio de um livro do tipo "Faça você mesmo".
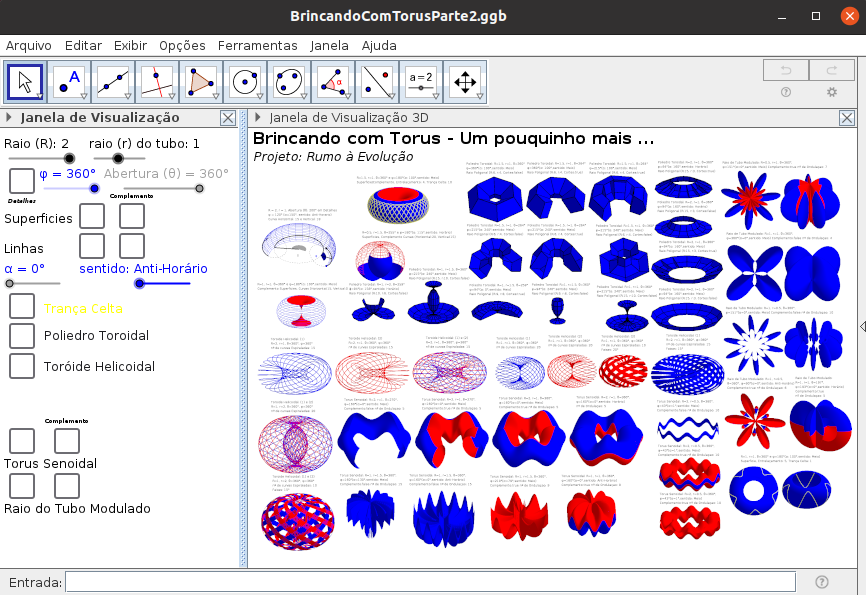
No projeto "Rumo à Evolução", apresentamos a segunda parte da aplicação Brincando com Torus. Nessa aplicação, para construir o Torus, definimos o Raio (R), o raio do Tubo (r), o ângulo de abertura (θ) referente ao raio R e o ângulo φ referente ao raio r. Para definir o ângulo φ, precisamos informar o ângulo α e o sentido (anti-horário, meio, horário). Em Detalhes, acompanhamos o passo a passo de toda a construção.
Assim, usando tais parâmetros, em Superfície temos a representação visual do Torus e quando selecionado complemento, temos o suplemento visual de Torus e relação a φ. Em Linhas, temos os arcos horizontais e verticais da representação visual e do suplemento de Torus. Tal situação acontece quando selecionamos a opção Torus Senoidal em que ondulamos o raio R e também quando ondulamos o raio r, na opção Raio de Tubo Modulado. Nessa opção é possível definir o número de ondulações.
Além disso, é possível desenhar senoides sobre a superfície do Torus. Para isso, selecionamos a opção Trança Celta e, em seguida, definimos a quantidade de Entrelaçamento e o número de Trança Celta. Note que, tais tranças acompanha o ângulo de abertura (θ) referente ao raio R.
Na opção Toroide Helicoidal, utilizamos os parâmetros iniciais, desenhamos o Torus por meio de Curvas Espiraladas. Para isso definimos a quantidade de curva e o sentindo, esquerda para direita (1) e/ou vice-versa (2). Visto que as curvas são formadas a partir do raio r, é possível obter superfícies nos dois sentidos: (1) e/ou (2) modificando o ângulo da faixa. Também é possível visualizar a animação do Toroide Helicoidal selecionando a opção Animar.
Finalmente, na opção Poliedro Toroidal, utilizamos os parâmetros iniciais, desenhamos poliedros a partir de polígonos obtidos por meio dos raios poligonais R e r. Quando o ângulo de abertura (θ) referente ao raio R vale 360° o polígono formado pelo raio poligonal R e quando o ângulo φ referente ao raio r é diferente de 360° é possível visualiza o polígono formado pelo raio poligonal r, e os cortes laterais quando o ângulo φ é diferente de 360°, formando assim, diferente tipos de figuras.
Enquanto o livro não está disponível, curta a página "Gifs Animados de Construções Geométricas" em http://www.facebook.com.br/almeidacrm/" e não seja o último a saber das novidades ainda não compartilhadas.