Rosa de Maurer - Maurer Rose
Projeto: Rumo à Evolução
Animações feitas no software livre de geometria dinâmica com o objetivo de valorizar os principais recursos das construções geométricas. A ideia original é apresentar um passo a passo explicando cada um dos comandos utilizados por meio de um livro do tipo "Faça você mesmo".
No projeto "Rumo à Evolução", apresentamos o conceito de rosa de Maurer introduzido por Peter M. Maurer em seu artigo intitulado "Uma rosa é uma rosa..." que consiste em algumas linhas que conectam alguns pontos em uma curva de rosa. Essa rosa é definida por r = sen(n θ), composta por 360 retas que conectam 361 pontos.
Assim, escolhendo o valor de n e um incremento de ângulo d (em graus) definimos o ponto P_i = (r(θ_i), θ_i) convertendo para coordenadas cartesianas e ligamos o ponto P_i com P_{i+1} por um segmento de reta obtendo uma trama intrincada que parece uma estrela ou mandala, dependendo de n e d.
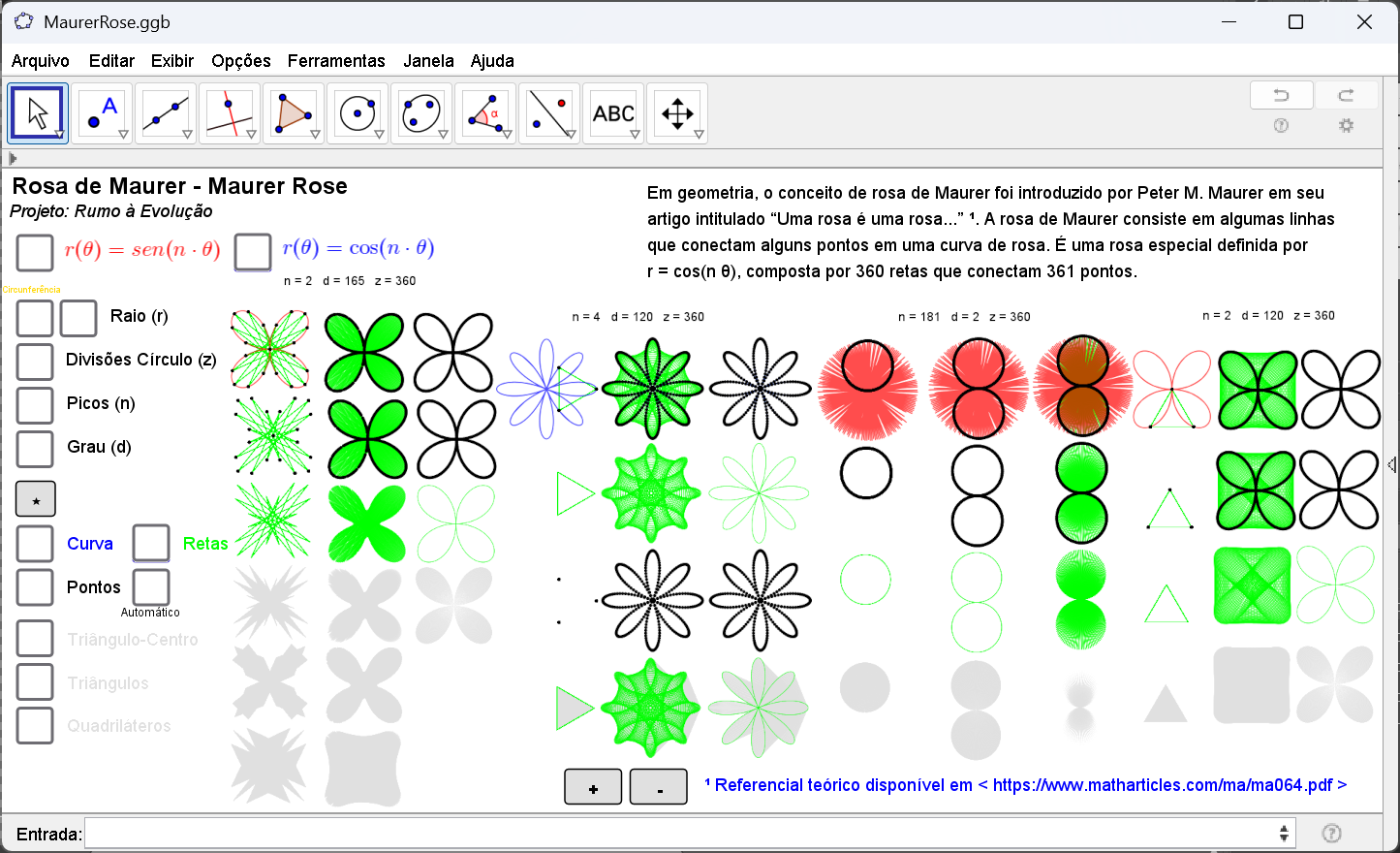
Nessa aplicação, temos as opções sen(n θ) e cos(n θ) em 3 algoritmos distintos, sendo: o Algoritmo A que é o algoritmo-base descrito no artigo com objetivo simples e que pode degenerar em casos "ruins"; o Algoritmo B que preenche lacunas, evitando degenerações e obtendo formas mais completas; e o Algoritmo C que generalizar o método, permitindo subdivisões diferentes de 360 (z), explorando novas formas visuais.
É possível exibir a rosa de Maurer na opção Curva, exibir o Círculo Tracejado na opção Circunferência e exibir individualmente ou coletivamentes cada um dos 361 pontos e das 360 retas clicando respectivamente nas opções Retas e/ou Pontos e Automático. Também temos as opções Triângulo-Centro, Triângulos e Quadriláteros usados para sobrepor formas poligonais nos pontos que facilita o estudo de padrões de conectividade, área, tesselações, etc.
Finalmente, caso não estejamos definindo o valor do raio (r), as divisões círculo (z), o Pico (n) e o Grau (d), é possível visualizar figuras mencionadas ao longo do artigo com valores fixos de n, d e z clicando nos botões + e -.
Enquanto o livro não está disponível, curta a página "Gifs Animados de Construções Geométricas" em http://www.facebook.com.br/almeidacrm/" e não seja o último a saber das novidades ainda não compartilhadas.
