La Tierra y el Sol
La Tierra y el Sol, coordenadas celestes, tiempo, solsticios, equinoccios, analema
Table of Contents
- La Tierra
- La Tierra, una plantilla
- Rotación, eje, polos y ecuador
- Latitud y paralelos
- Longitud y meridianos
- Las antípodas
- Coordenadas geográficas
- Loxodrómica (rumbo fijo)
- Ortodrómica (recorrido mínimo)
- La Tierra (ciudades, referencias, curvas...)
- Mapa mudo
- El mapa de Mercator
- El Sol
- Órbitas elípticas
- Trópicos y círculos polares
- Reloj solar
- Tiempo Universal Coordinado
- Países y zonas horarias
- Sol y Tierra (sistema de coordenadas celestes)
- Esfera armilar
- La Luna
- Tierra, Sol y Luna
- Fases lunares
- Aristarco de Samos
- Sol y Luna: tamaño aparente
- Luna: tamaño y distancia
- Sol: tamaño y distancia
- Venus
- La flor de Venus
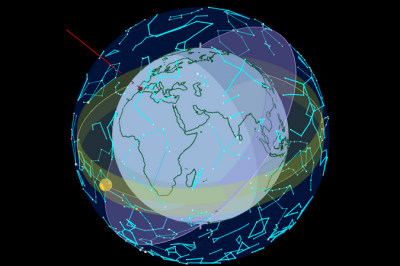
La Tierra, una plantilla
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra[/i] [url=https://www.geogebra.org/m/BEUGAvQj]La Tierra y el Sol[/url].[br][br][/color]Intenta envolver una pelota con papel de regalo y te darás cuenta que debido a su "curvatura en todas direcciones" siempre quedarán espacios entre la pelota y el papel, es imposible un ajuste perfecto.[br][br]Para simplificar, supondremos que la forma de la Tierra es perfectamente esférica. Para una representación lo más fiel posible de la Tierra lo mejor es usar un globo terráqueo, pues aquí pasa como al envolver la pelota, cualquier intento de "aplanar" la superficie terrestre conllevará siempre algún tipo de deformación, algún tipo de desviación de las medidas correctas (ya sea distancias, ángulos o áreas).[br][br]Esto se debe a que la esfera no se puede "desarrollar", es decir, no se puede extender su superficie sobre el plano. La siguiente imagen corresponde a un mapamundi. Reconocemos el perfil de los continentes, pero al ser una imagen plana, en vez de una superficie esférica, sabemos que necesariamente debe estar deformada. Todos los mapamundi, de alguna forma, "mienten".
En este caso, se ha "pintado" la superficie esférica como si la Tierra fuera un cilindro que rodase sobre el papel (esta forma de proyectar se llama [url=https://www.geogebra.org/m/xp33qgxu#chapter/596017]proyección cilíndrica[/url] y, aplicada a la Tierra, se conoce como [url=https://www.geogebra.org/m/ezbz88uz]proyección de Mercator[/url]). Observa que el Ártico (cuya masa de hielo aparece representada como un sólido más) y la Antártida aparecen exageradísimos, pues tanto el Polo Norte como el Polo Sur ocupan todo el largo de la imagen, en vez de un punto.
Por estas razones es recomendable disponer de una plantilla del globo terráqueo sin recurrir al mapamundi, como la que muestra la siguiente construcción.
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Órbitas elípticas
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra[/i] [url=https://www.geogebra.org/m/BEUGAvQj]La Tierra y el Sol[/url].[/color][b][br][br]Proyecto 2D[/b]: [i]modelizar el movimiento orbital terrestre.[/i][br][br]Colocamos el punto S (Sol) en el centro de coordenadas y un punto T (Tierra) con velocidad inicial el vector v. Si d es la distancia TS y k es una constante, tenemos el vector de fuerza gravitatoria: [br][br] g = k / d² VectorUnitario(Vector(T, S))[br][br]Ahora solo hay que introducir un deslizador auxiliar para que, cada vez que se actualice, ejecute el simplísimo guión:[br][br] Valor(T, T + 0.01 v)[br] Valor(v, v + 0.01 g)[br][br]¡Y ya tenemos el movimiento elíptico! (Obsérvese que no hemos empleado ninguna ecuación ni lugar geométrico.)
En la siguiente construcción podemos ver una versión más amplia, con la velocidad de escape y la conservación de la energía mecánica.[br]
Nota: Estas dos construcciones fueron realizadas gracias a la ayuda de mi compañero de departamento Julio Valbuena Herrero, quien adaptó la idea expuesta por Richard Feynman en su famoso lilbro [i]The Feynman Lectures on Physics[/i] (1963, [url=https://www.utnianos.com.ar/foro/attachment.php?aid=7332]volumen I[/url], 9-7, [i]Planetary motions[/i]).
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Tierra, Sol y Luna
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra[/i] [url=https://www.geogebra.org/m/BEUGAvQj]La Tierra y el Sol[/url].[/color][br][br]En esta construcción puedes observar el posicionamiento, relativo a la Tierra, del Sol y la Luna. En el panel de la izquierda se muestra la fase correspondiente de la Luna, vista desde la Tierra. Ten en cuenta que la visualización de esa fase depende de la latitud del observador sobre la Tierra (latitud del punto rojo). Por ejemplo, en el cuarto creciente, si centras la vista de la Tierra en el Polo Norte aparece la Luna "a la derecha" del Sol, pero al centrar la vista en el Polo Sur, la misma Luna aparecerá "a la izquierda" del Sol.[br][br]Observa que la Luna no se encuentra, habitualmente, sobre la eclíptica, sino algo por debajo o por encima de ella. Su órbita, que varía con el paso del tiempo, forma con la eclíptica un ángulo de unos 5° y la corta solo en dos puntos, llamados [i]nodos[/i]. Los eclipses de Sol [url=https://astronoo.com/images/soleil/grains-de-baily.jpg][img]https://www.geogebra.org/resource/scjbyz2p/0tuzuVw455vxurEw/material-scjbyz2p.png[/img][/url] solo son posibles cuando la Luna está en un nodo (o próxima a él) y se encuentra entre la Tierra y el Sol, ya que, en un eclipse solar total, el observador debe estar alineado con los centros de la Luna y el Sol.
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Sol y Luna: tamaño aparente
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra[/i] [url=https://www.geogebra.org/m/BEUGAvQj]La Tierra y el Sol[/url].[/color][br][br]Esta es la primera de tres actividades en las que podrás comprobar la utilidad de la trigonometría para poder realizar mediciones sobre objetos inaccesibles, incluso muy distantes, como las estrellas. De hecho, la trigonometría es fundamental en Astronomía, a la que sirve desde hace milenios. Hoy las relaciones trigonométricas se encuentran presentes en multitud de cálculos y las funciones trigonométricas son esenciales para el análisis de muchos fenómenos físicos.[br][br][table][tr][td][img]https://www.geogebra.org/resource/yzf5aw3k/fAnAgQhXjyenEnwV/material-yzf5aw3k.png[/img][/td][td]Reproduciremos el método que usó el matemático griego [b]Aristarco[/b] (siglo III a.C.), tal vez el primero en proclamar que la Tierra orbita alrededor del Sol, para calcular el tamaño de la Luna y el Sol, así como la distancia que nos separa de ambos. [br][br]En la imagen puedes ver uno de los dibujos de los que se ayudó.[/td][/tr][/table][br]En esta primera actividad podrás comprobar cómo con la simple observación directa, sin sofisticados instrumentos, el astrónomo y matemático griego Aristarco consiguió medir el tamaño aparente de la Luna y Sol en el cielo, es decir, determinar el valor del ángulo con el que los vemos. [br][br]El esquema que aparece en la aplicación muestra el escenario desde un punto de vista situado en la vertical del polo Norte solar. Tanto la Tierra como la Luna orbitan con movimiento directo, es decir, en sentido antihorario desde ese punto de vista. Para simplificar, el Sol se mantiene fijo y la Tierra no gira sobre su eje, ya que el movimiento del Sol y la rotación de la Tierra no intervienen en nuestros cálculos. [br][br]Nota: la luna llena y la luna nueva no siempre se encuentran alineadas con la Tierra y el Sol porque el plano en el que orbita la Luna está algo inclinado respecto al plano en el que orbita la Tierra. Por este motivo no hay un eclipse total de Sol todos los meses.[br][br]Puedes mover la Tierra y la Luna arrastrando sus centros.
1. En la aplicación los tamaños relativos de la Tierra y la Luna son los reales. ¿Está el Sol también representado con la misma escala?
2. ¿Crees que la distancia de la Luna a la Tierra está representada a escala? Es decir, ¿crees que la proporción entre esa distancia y el tamaño de la Tierra y la Luna es la real?
3. La aplicación no muestra un dibujo a escala (salvo la proporción entre los tamaños de la Tierra y la Luna), sino de un esquema similar al que realizó Aristarco como ayuda a sus observaciones y razonamientos.[br][br]Activa la casilla "Eclipse de Sol". Desde la Tierra, la Luna oculta al Sol casi con completa precisión en un eclipse total. Aristarco dedujo que entonces vemos ambos astros con el mismo ángulo, es decir, tienen el mismo tamaño aparente. ¿Por qué?
4. Activa la casilla "Eclipse de Luna". Aristarco observó que desde que comenzaba un eclipse de Luna hasta que la sombra de la Tierra cubría por completo la Luna pasaba una hora, aproximadamente. Es decir, en una hora la Luna recorre todo su diámetro.[br] [br]Aristarco sabía, observando la periodicidad de las fases lunares, que la Luna tarda 29.5 días en dar una vuelta completa a la Tierra. Así dedujo que el ángulo con que vemos la Luna (o el Sol) es de 0.51º, aproximadamente. ¿Por qué?
5. Teniendo ese ángulo en cuenta, así como la definición de tangente de un ángulo, ¿cuántas veces el radio [b]R[/b] del Sol debe ser la distancia [b]D[/b] hasta él?
6. ¿Cuántas veces el radio [b]r [/b]de la Luna debe ser su distancia [b]d[/b] hasta ella?
[color=#999999]Autor de la construcción y la actividad: Rafael Losada Liste. [br]Esta actividad está presente en el [url=http://geogebra.es/gauss/]Proyecto Gauss[/url][/color]
La flor de Venus
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra[/i] [url=https://www.geogebra.org/m/BEUGAvQj]La Tierra y el Sol[/url].[/color][br][br]Cada 8 años, Venus da casi exactamente 13 vueltas alrededor del Sol. En ese tiempo, Venus adelanta 5 veces a la Tierra, generando una cáustica que recuerda a 5 cardioides entrelazadas (sería una cardioide si el año terrestre durase el doble que el venusiano). [br][br][table][tr][td][img]https://www.geogebra.org/resource/e7mpzznx/Vgj1tg6hCd19WqgG/material-e7mpzznx.png[/img][/td][td]Más precisamente, la fracción de los [url=http://www.geogebra.es/060419/img/ciclo%208%20a%C3%B1os.jpg]períodos orbitales[/url] entre ambos planetas (365,256/224,701) está muy próxima a ser 13/8 (1+5/8). Por tanto, el ciclo relativo se repite cada 8/5=1,6 años, que equivale a 576º (una vuelta y 216º) de vueltas terrestres, lo que provoca la aparición de ese patrón pentagonal conocido como pentagrama o flor de Venus.[/td][/tr][/table] [br][table][tr][td][img]https://www.geogebra.org/resource/d7bbv2za/m36LgTXqSZEHI7SP/material-d7bbv2za.png[/img][/td][td]Como las trayectorias de Venus y la Tierra son casi circunferencias, obtenemos el mismo diagrama sustituyendo el segmento Tierra-Venus por su punto medio PM. También obtenemos el mismo diagrama como un [url=http://www.geogebra.es/060419/img/flor%20de%20venus%20punto%20medio.png]epiciclo [/url]de Venus visto desde la Tierra, sin más que ajustar la escala de las distancias a la mitad. Esto se debe a que si sumamos la mitad del vector Sol-Tierra con la mitad del vector Sol-Venus, obtenemos precisamente el vector Sol-PM.[/td][/tr][/table] [br][table][tr][td][img]https://www.geogebra.org/resource/vpcqyxsx/rXrlf28nOmBZ0umL/material-vpcqyxsx.png[/img][/td][td]Suponiendo que las trayectorias de Venus y la Tierra fueran circunferencias perfectas y la relación 13/8 fuera exacta, la flor de Venus sería una [b]epitrocoide [/b]perfecta, es decir, podría ser generada por una gigantesca rueda que rodase (sin deslizamiento) sobre un círculo centrado en la Tierra con radio 5/13 de la distancia de la Tierra al Sol. [/td][/tr][/table] [br]En la construcción, PULSA EL BOTÓN REPRODUCIR (esquina inferior izquierda, apenas se ve).[br]
Notas:[br][br][table][tr][td][img]https://www.geogebra.org/resource/rhwwjvbh/TJunsL6A6rdbQK1K/material-rhwwjvbh.png[/img][/td][td][img]https://www.geogebra.org/resource/ggcedbyb/mnhPrkVenfaqpCDk/material-ggcedbyb.png[/img][/td][td]1. La flor de Venus se puede materializar fácilmente mediante hilos tensados ([url=http://www.geogebra.es/060419/img/hilorama%20flor%20de%20venus.png]hiloramas[/url]). Es muy conocido por los aficionados a la astrología y otras pseudociencias, de modo que se puede encontrar su diseño en todo tipo de objetos, como en [url=http://www.geogebra.es/060419/img/joyer%C3%ADa%20flor%20de%20venus.jpg]joyería[/url].[/td][/tr][/table][table][tr][td][img]https://upload.wikimedia.org/wikipedia/commons/thumb/0/0e/Cassini_apparent.jpg/250px-Cassini_apparent.jpg[/img][br][br][/td][td]2. La imagen del diagrama que aparece en la construcción proviene de la entrada "epiciclo" en Wikipedia - Movimiento aparente (J. Ferguson 1710-1776 basado en un diagrama similar de G. Cassini 1625-1712).[br][/td][/tr][/table][br]3. La construcción ha sido realizada con los datos reales de la Tierra y Venus, pero se puede simplificar mucho usando circunferencias en vez de elipses, sin que se aprecie diferencia alguna dada su pequeña excentricidad. También se puede usar directamente la relación 13/8.
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]