Día GeoGebra 2025
Programa Día GeoGebra 2025

Enlace a esta presentación

Dibujar funciones
Introduce la función que quieres que se dibuje.[br]Se puede marcar un tramo de la función, moviendo las dos flechas que hay sobre el eje "x"[br]Puedes usar el "analizador de funciones" para estudiar algunas propiedades; también puedes agregar texto o dibujar algo con el ratón.
Actividades CAS para el aula. Ejemplos
Divisibilidad
1. Factoriza el número 3824[br]2. Calcula el cociente y el resto de la división de 7834 entre 457.[br]3. Es primo el número 239 y 23429[br]4. Calcula el número de divisores que tiene el número 548.[br]5. Calcula los divisores de 5328.[br]6. Calcula la suma de los divisores de 725.[br]7. Calcula el Máximo Común Divisor y el Mínimo Común Múltiplo de 28 y 62.
Polinomios
Asigna a las letras p y q los siguientes polinomios respectivamente.[br][b][center]P(x)=x[sup]4[/sup]-9x[sup]3[/sup]+26x[sup]2[/sup]-24x y Q(x)= (x-2)[sup]2 [/sup](x[sup]3[/sup]-1)[/center][/b]1. Factoriza el el polinomio P(x).[br]2. Desarrolla el polinomio Q(x).[br]3. Calcula el cociente y el resto de la división de P(x) entre Q(x).[br]4. Calcula el Máximo Común Divisor y el Mínimo Común Múltiplo de P(x) y Q(x).[br]5. Calcula el valor de P(x) en x=3.
Ecuaciones
1.Resuelve la ecuación x[sup]2[/sup] - x - 1=0[br]2. Resuelve la ecuación: (x[sup]2[/sup] -1)[sup]2[/sup](x-1)=2x+3 utilizando diferentes comandos y heramientas.[br]3. Resuelve la ecuación : (x[sup]2[/sup] -1)[sup]2[/sup](x-1)=2x+3 incluyendo la forma gráfica.[br]4. Resuelve la ecuación general de segundo grado.
Inecuaciones
1. Resuelve la inecuación 2x−7⩾−x+3[br]2. Resuelve la inecuación x[sup]3[/sup]−3 x+7> x[sup]2[/sup]−2[br]3. Resuelve las dos inecuaciones anteriores gráficamente.
Sistemas de ecuaciones
[list=1][*]Resuelve los siguientes sistemas analítica y geométricamente:[br][list=a][*][br][math]\Large\left\{\begin{array}{ccl}[br]3x+2y&=&17\\[br]5x-y&=&11[br]\end{array}\right.[/math][br][/*][br][*][math]\Large\left\{\begin{array}{ccl}[br]3x^2-5y^2&=&30\\[br]x^2-2y^2&=&7[br]\end{array}\right.[/math][br][/*][/list][/*][*]Discute y resuelve el siguiente sistema [math]\Large\left\{\begin{array}{ccl}[br]2x+y-z&=&0\\[br]x+3y+2z&=&5\\[br]x-y+4z&=&9[br]\end{array}\right.[/math][/*][br][*]Discute y resuelve el siguiente sistema para los distintos valores de m: [math]\Large\left\{\begin{array}{ccl}[br]x+my+z&=&1\\[br]mx+y+(m-1) z&=&m\\[br]x+y+z&=&m+1[br]\end{array}\right.[/math][br][/*][*]Discute y resuelve según los valores de a: [math]\Large\left\{\begin{array}{ccl}[br]x-2y+az&=&a\\[br]x+4y+a^2z&=&6+a\\[br]x-8y+a^2z&=&-6[br]\end{array}\right.[/math][br][/*][br][/list][br]
Estudio de funciones
[list=1][*]Representa la recta y=mx+n y hazla variar gráficamente en función de la pendiente y la ordenada en el origen.[/*][*]Representa la parábola y= a(x-b)[sup]2[/sup]+b y hazla variar en función de los valores a, b y c.[br][/*][*]Representa la función [math]\large y= \frac{1}{x−b}+c[/math] y hazla variar en función de los valores b y c. [br][/*][*]Representa las asíntotas.[br][/*][*]Haz un estudio rápido y global de la función f(x) = x[sup]3[/sup]-3x[sup]2[/sup]+x+3.[br][/*][*]Realiza el estudio de la función.[br][/*][/list]
Derivadas
[list=1][*]Calcula la derivadas sucesivas de la función f(x) = x[sup]3[/sup]-3x[sup]2[/sup]+x+3.[br][/*][*]Calcula la recta tangente a la función anterior en un punto cualquiera A de la curva.[br][/*][*]Calcula los extremos relativos y los puntos de inflexión de la función anterior con la ayuda del cálculo de derivadas.[/*][*]Calcula la derivada de la función que estamos estudiando como lugar geométrico.[br][/*][*][b]Optimización[/b]. Aprovechando como hipotenusa una pared de 15 metros un pastor desea acotar una superficie triangular. ¿Qué medidas deberán tener los otros dos lados del triángulo (catetos) con objeto de obtener una superficie máxima?[/*][/list]
Integrales
[list=1][*]Calcula la integral indefinida de la función f(x) = x sen(x)[br][/*][*]Calcula la integral definida de la función anterior en el intervalo [-5,5].[br][/*][*]Calcula la integral definida de la función f(x) = x sen(x) entre dos valores cualesquiera A y B.[br][/*][*]Calcula el área limitada por la funciones f(x) = x sen(x) y g(x) = x[sup]2[/sup] – 5x + 6 entre dos puntos de corte.[/*][/list]
Arcos de medio punto, escarzanos, de herradura, apuntados...
Los [url=http://enciclopedia.us.es/index.php/Arco_(arquitectura)]arcos[/url] de circunferencia son muy utilizados en construcciones. Los puntos en los que el arco se apoya el arco se llaman "impostas". La distancia entre las impostas se denomina "luz"[br][list][*]Los romanos solían utilizar medias circunferencias, y el arco se denominaba "de medio punto", de manera que el centro de la circunferencia está precisamente en la línea que une las impostas, y comprende un ángulo llano. Su altura es, precisamente, la mitad de su luz.[br][/*][*]Cuando el centro está por debajo de la línea de impostas, el arco se denomina "[url=https://es.wikipedia.org/wiki/Arco_escarzano]escarzano[/url]", y comprende un ángulo menor de 180º. Por tanto, es un arco rebajado (su[i] [/i]altura es menor que la mitad de su luz).[/*][*]Si el centro está por encima, el arco se denomina "de [url=https://es.wikipedia.org/wiki/Arco_de_herradura]herradura[/url]", y es un arco "ultrapasado" (altura mayor que la mitad de su luz).[/*][/list][br]
Arco de circunferencia que modeliza el arco escarzano "[url=https://cacereshistorica.caceres.es/patrimonio-historico/edificios-historicos/arquitectura-civil/arco-de-la-estrella-o-puerta-nueva/]Arco de la Estrella[/url]", en Cáceres.[br][br]Debajo, la imagen original (descargar para repetir esta construcción).[br][br][b]Ejercicio[/b]: buscar imágenes de otros arcos escarzanos, de medio punto o de herradura, y modelizarlos de la misma forma.
Arco de la Estrella, en Cáceres

Arco Carpanel de Tres Centros
Para disminuir el ángulo que forma el arco rebajado con las impostas, podemos añadir unas circunferencias tangentes tanto a ese primer arco como a los laterales. En particular, el centro de estos nuevos arcos debe estar en la línea de impostas.[br][br]Así, obtenemos un arco formado a su vez por tres arcos de circunferencia, que denominamos Arco Carpanel (de tres centros). En [url=https://www.geogebra.org/m/xttthtwe]este enlace[/url] puedes aprender más detalles sobre cómo crear este tipo de arcos.[br]En ocasiones, pueden añadirse más circunferencias.
Arco Carpanel en una casa
Imagen para modelizar

Arco típico en los pasillos de las casas de los pueblos de la Siberia Extremeña (España). Concretamente, Tamurejo.
Ejercicio. Fachada del CPR de Cáceres
La siguiente fotografía es de la fachada del CPR de Cáceres.[br]Podemos identificar diferentes elementos matemáticos, dependiendo de en qué nos interese centrarnos.[br]Analiza estos elementos utilizando GeoGebra.[br]Por ejemplo:[br][list][*]La pequeña rampa de entrada, combinada con los escalones, sirven para el estudio de la [b]pendiente de una recta[/b].[/*][*]Las propias escaleras, para analizar las rectas [b]paralelas[/b].[/*][*]El hecho de que la foto se tomó con un pequeño [b]ángulo[/b], hace que "sobre el papel", el ángulo de los laterales y las escaleras no sea del todo recto, pero ¿nos aporta información sobre el ángulo que estaba haciendo la cámara con la vertical respecto al suelo mientras se tomaba la fotografía?[/*][*]¿Qué figuras geométricas con las lámparas interiores? [/*][*]¿Y las piedras del contorno? Analiza qué herramientas matemáticas y de GeoGebra utilizaríamos para modelizarlas.[/*][/list]Pero queríamos centrarnos en el estudio de los arcos. Para ello, lo analizaremos de la siguiente manera:[br][list][*]¿Cómo trazar el primer arco de la izquierda? (describe matemáticamente, y llévalo a cabo)[br]Repite la actividad de manera que quede patente que es un arco de medio punto.[/*][*]El arco central, ¿es igual que el de la izquierda? ¿Qué estrategias matemáticas podemos llevar a cabo para mostrarlo?[/*][*]¿Y con el tercero?[/*][*]La parte superior del arco, ¿qué tipo de circunferencia formaría respecto la parte inferior?[/*][/list]

Entrada al CPR de Cáceres.
Comparando arcos
La siguiente imagen es del patio del edificio del Palacio de Toledo-Moctezuma de Cáceres, donde se encuentra el actual Archivo Histórico Provincial.[br][list][*]Podemos apreciar la diferencia entre un arco escarzano y uno de medio punto. Ambos tienen la misma flecha (altura), pero diferente luz (ancho). [/*][*]Añadiendo un poco más de curvatura en los extremos del arco escarzano, lo transformaríamos en un arco carpanel de tres centros.[/*][*]Vamos a observar las diferencias en la construcción. Compara las posiciones de los centros de las circunferencias y cómo varía el arco carpanel al modificar la posición del centro.[/*][/list][size=85](*) Recuerda que puedes visitar [url=https://www.geogebra.org/m/xttthtwe]esta actividad[/url] para aprender más sobre la construcción del arco carpanel.[/size]
Palacio de Toledo-Moctezuma
Otros arcos para modelizar
Aquí tienes otras imágenes que puedes utilizar para modelizar diferentes tipos de arco.[br][br]

Fachada de una casa de Siruela (Badajoz)
Una mirada matemática en la Plaza Alta de Badajoz
Las siguientes fotografías han sido tomadas en la Plaza Alta Marín de Rodezno, de Badajoz (España). [br][[url=https://goo.gl/maps/x5pXPBuPdDhv7Dp9A]Clic para ir a Google Maps[/url]]
Fachada de las Antiguas Casas Consistoriales de la Plaza Alta de Badajoz

Arco del Peso en la Plaza Alta de Badajoz

Al fondo, tras el arco, se ve la fachada del Convento de San José.
Convento de San José de Badajoz

Es habitual que combinar diferentes tipos de arco.
LaTeX en GeoGebra
LaTeX también en rótulos
Se puede utilizar LaTeX en los rótulos (por ejemplo de los botones) o dentro de las listas desplegables.[br]Tan solo hay que poner el comando entre símbolos de dólar que es lo que se ha hecho en el botón "Fórmulas [math]\textcolor{brown}{\sqrt{x},\frac{a}{b}}[/math]" , cuyo rótulo es (dólar)\text{Fórmulas \textcolor{brown}{\sqrt{x},\frac{a}{b}}(dólar)
Para más información, visitar la [url=https://wiki.geogebra.org/es/Sobre_LaTeX_-medidas_de_fuentes_-_cajas_de_color_y_matem%C3%A1tica_-]wiki de GeoGebra[/url] sobre LaTeX, o la recopilación de ejemplos [url=https://www.geogebra.org/m/RC7Pnnk5]https://www.geogebra.org/m/RC7Pnnk5[/url], de [url=https://www.geogebra.org/u/michael+borcherds]Michael Borcherds[/url].[br][br]Más nombres de colores en [url=https://en.wikibooks.org/wiki/LaTeX/Colors#The_68_standard_colors_known_to_dvips]este enlace (wikibooks)[/url]. Para usar los colores predefinidos LaTeX, podría hacerse así: \textcolor{ProcessBlue}{Hola}[br][br]En este [url=https://oeis.org/wiki/List_of_LaTeX_mathematical_symbols]enlace de oeis.org[/url] hay una lista de los principales símbolos matemáticos en LaTeX.[br]
¿Cuánto vale cada imagen?
Introduce el resultado en la casilla y pulsa el botón "corregir".[br]¿Podrás resolver 4 fichas?
Para ampliar conocimientos
Este applet forma parte del recurso educativo '[url=https://emtic.educarex.es/crea/matematicas/numerosnaturales/index.html]Juegos Matemágicos con Números Naturales[/url]', del [url=https://emtic.educarex.es/proyectocrea-mates]proyecto CREA[/url] de la Consejería de Educación y Empleo de la Junta de Extremadura (España).
Ejercicios: Elementos Geométricos
Mediante comandos o las herramientas, podemos calcular perpendiculares, paralelas, mediatrices, bisectrices,... Por ejemplo:[br][list][*]Con [icon]https://www.geogebra.org/images/ggb/toolbar/mode_polygon.png[/icon] creamos un [b]triángulo[/b].[/*][*]Calculamos la [b]mediatriz[/b] de cada lado con [icon]/images/ggb/toolbar/mode_linebisector.png[/icon][/*][*]Marcamos su [b]intersección[/b] (circuncentro) con [icon]/images/ggb/toolbar/mode_intersect.png[/icon][/*][*]Trazamos la circunferencia circunscrita [icon]/images/ggb/toolbar/mode_circle2.png[/icon].[br][/*][/list]Por supuesto, la construcción es dinámica. Si movemos los puntos, todo se recalcula directamente.[br][br]Puedes probar a hacer la construcción [url=https://www.geogebra.org/geometry]aquí (https://www.geogebra.org/geometry)[/url].
Vídeos explicativos
En los siguientes vídeos veremos cómo construir con GeoGebra algunos de los elementos notables del triángulo:[br][list][*][url=https://drive.google.com/open?id=1RukQ6-SqCao2PfaFSiONNV_LSiiLk5wt]Medianas y baricentro[/url].[/*][*][url=https://drive.google.com/open?id=1wTJ2OULTzLILmQr7Z4q0phBlk5rfUKRp]Mediatrices, circuncentro y circunferencia circunscrita[/url].[/*][*][url=https://drive.google.com/open?id=14wbQo7NYWA0c37cvwuc84wLUQEDRSXOT]Alturas y ortocentro[/url].[/*][*][url=https://drive.google.com/open?id=1pLTvYfw4ChfcOqjnxCTMfXDsmlVaentY]Bisectrices, incentro y circunferencia inscrita[/url].[/*][/list]
Término general de una progresión aritmética
Instrucciones
[list][*]Cada apartado vale 2,5 puntos. Utiliza la letra "n" para el término general. [br][/*][*]No se penaliza el uso de paréntesis.[/*][*]Si introduces una expresión no válida y aparece un mensaje de error, tendrás que pulsar "Hacer otro" un par de veces, para que se vuelva a reconocer las sucesiones correctamente.[br][/*][/list]
Para saber más
Las siguientes cuestiones que podríamos preguntarnos son[br][list][*]¿cómo hacer para averiguar cuál es la progresión, si nos falta algún término?[/*][*] ¿cuál es la suma de todos los términos que aparecen?[/*][/list]Para resolverlo, también disponemos de procedimientos matemáticos, que podemos practicar en las actividades [url=https://www.geogebra.org/m/HJVA6BD4]Progresiones aritméticas con términos que faltan[/url] y [url=https://www.geogebra.org/m/r7fgvgdq]Progresiones aritméticas. Suma de términos[/url].
Nuestro turno para reflexionar

Vamos a fijarnos en la foto de las pesas del gimnasio. ¡Pero si cada fila está colocada en progresión aritmética![br][list][*]¿Podrías encontrar el término general de cada una? Ten en cuenta que las mancuernas están repetidas, pero puedes pensar que cada término se refiere a "pareja de mancuernas".[/*][*]¿De cuánto peso son las mancuernas que no se ven?[/*][*]¿Cuánto peso hay en total? Ojo, que para dar la solución debemos tener en cuenta que cada peso está repetido.[/*][/list]
MatesGG: Matemáticas con GeoGebra

[url=https://intef.es/recursos-educativos/matesgg/]MatesGG[/url]
La Federación Española de Sociedades de Profesores de Matemáticas ([url=https://fespm.es/]FESPM[/url]) en colaboración con el Instituto Nacional de Tecnologías Educativas y de Formación del Profesorado ([url=https://intef.es/]INTEF[/url]) y el Centro Internacional de Encuentros Matemáticos ([url=https://www.ciem.unican.es/]CIEM[/url]) ha desarrollado el proyecto [url=https://intef.es/recursos-educativos/matesgg/]MatesGG[/url].[br][br]Es un espacio en el que se pone a disposición del profesorado una selección de materiales elaborados con la herramienta GeoGebra a través de unas guías didácticas creadas con la herramienta de autor eXeLearning.[br][br]En estas guías, el profesorado encontrará información detallada sobre el recurso: información curricular, propuestas de uso, material complementario, el archivo fuente de la guía (gracias al cual podremos editar, modificar y adaptar la guía a nuestras necesidades), así como el propio recurso en modo interactivo.
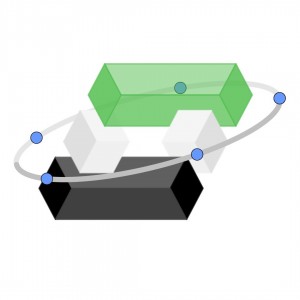
Nopertedro - adorno de Navidad
Esta propuesta navideña está basada en la actividad "Nopertedro" (https://www.geogebra.org/m/rt26dp3j). Visitar el enlace para conocer esta figura, que fue ideada en 2025 para resolver un curioso problema de matemáticas.[br]También, en esa ficha se sugieren algunas actividades relacionadas.
Nopertedro navideño
¿Cómo imprimir en 3D nuestra figura?
Una de las formas más habituales para imprimir una figura en 3D es a partir de un archivo .stl[br]GeoGebra permite descargarlo con la opción "Exportar como", dentro del menú desplegable con las tres rayas ≡ de la zona superior derecha.[br][list][*]Es posible que antes de dar a "Exportar como", tengas que hacer un poco de scroll en la pantalla, para que quepan todas las opciones. (Ver imagen adjunta).[/*][*]Tras pulsar ahí, elegimos en el menú las dimensiones finales con las que queremos que se genere nuestra figura y ¡listo![/*][*]Una vez tengamos el archivo .stl, basta con subirlo a nuestro software para laminar, que nos genere el archivo gcode que podamos llevar a la impresora 3D.[/*][/list]