Himmelsmechanik
Table of Contents
- Planetenbahnen
- 2. Kepler Gesetz
- Arbeiten von J. Kepler
- Die Keplersche Fassregel - Teil 2
- Kepler-Fernrohr
- Weiteres
- Analemma
- Analemma 3D
- Heliozentrisches Weltbild
- Bahn der Sonne
- Kalender
- Sonnenaufgang und Sonnenuntergang
- Mond
- Sonne- und Mondfinsternis
- Earth and Moon
- Sonnensystem
- Sonnensystem
- Sonnensystem in 3d
- Sonne - Erde - Mond in 3D
- Bahnschleifen
- Satelliten
- Fluchtgeschwindigkeit
- Übersicht eines Satelliten
- Earth and Sun
- Earth (basic model)
- Earth (cities, references, curves...)
- Earth and Sun (celestial coordinate system)
- Jahreszeiten
- Erde, Sonne, Jahreszeiten
2. Kepler Gesetz
Die Keplersche Fassregel - Teil 2
Die Keplersche Fassregel dient zur näherungsweisen Berechnung eines bestimmten Integrals.[br][br]Keplersche Fassregel [math]\int_{a}^{b} f\left(x\right)dx\approx\frac{b-a}{6}\cdot\left(f\left(a\right)+4\cdot f\left(\frac{a+b}{2}\right)+f\left(b\right)\right)[/math][br][br][b]Aufgabe[/b][br]Weise mitilfe des CAS nach, dass die Keplersche Fassregel für Polynomfunktionen bis 3. Grades den exakten Wert des Integrals ergibt.[br]Erkläre anschaulich, warum der Flächeninhalt unter dem Graphen einer Polynomfunktion 3. Grades durch den Flächeninhalt unter einer Parabel berechnet werden kann.
Warum die Kepler'sche Fassregel auch für Polynomfunktionen 3. Grades gilt, veranschaulicht das folgende Applet.[br]Eine Polynomfunktionen 3. Grades kann in einem beliebigen Intervall [a; b] durch eine Polynomfunktionen 2. Grades ersetzt werden, wobei der das Integral von a bis b dabei unverändert bleibt.[br]Und das Integral für diese Polynomfunktionen 2. Grades kann durch die Funktionswerte an den Stellen a, b und in der Mitte von a und b berechnet werden.
Kepler'sche Fassregel für quadratische Funktionen
Die Kepler'sche Fassregel gilt für quadratische Funktionen nicht nur näherungsweise sondern ist eine exakte Berechnungsmöglichkeit.[br]Sei f auf [a; b] definiert und sei [math]m=\frac{a+b}{2}[/math] das arithmetische Mittel von a und b. Dann gilt[br][math]\int_a^b f\left(x\right)dx=\frac{b-a}{6}\cdot\left( f\left(a\right)+4f\left(m\right)+f\left(b\right)\right)[/math][br][br][b]Beweis[/b][br]Sei [math]f\left(x\right)=A\cdot x^2+B\cdot x+C[/math].[br][math]\int_a^bf\left(x\right)dx=\int_a^b\left(A\cdot x^2+B\cdot x+C\right)dx=\left(A\cdot\frac{x^3}{3}+B\cdot\frac{x^2}{2}+C\cdot x\right) \Bigg|_a^b = \frac{A}{3} \cdot \left(b^3-a^3\right)+\frac{B}{2}\left(b^2-a^2\right) + C\cdot (b - a) =[/math][br] [math]=\frac{b-a}{6}\cdot\left(2A\cdot\left(b^2+ba+a^2\right)+3B\cdot\left(b+a\right)+6C\right)[/math][br]Aus [math]m=\frac{a+b}{2}[/math] folgt [math]2m=a+b[/math] und nach Quadrieren [math]ab=\frac{4m^2-a^2-b^2}{2}[/math]. [br]Damit ergibt sich für das Integral [br] [math]=\frac{b-a}{6}\cdot\left(2A\cdot\left(b^2+\frac{4m^2-a^2-b^2}{2}+a^2\right)+B\cdot\left(b+a\right)+2B\cdot\left(b+a\right)+6C\right)=[/math][br] [math]=\frac{b-a}{6}\cdot\left(2Ab^2+4Am^2-Aa^2-Ab^2+2Aa^2+Bb+Ba+4Bm+6C\right)=[/math][br] [math]=\frac{b-a}{6}\cdot\left(\left(A\cdot a^2+B\cdot a+C\right)+\left(4A\cdot m^2+4B\cdot m+4C\right)+\left(A\cdot b^2+4B\cdot b+C\right)\right)=[/math][br] [math]=\frac{b-a}{6}\cdot\left(f\left(a\right)+4\cdot f\left(m\right)+f\left(b\right)\right)[/math]
Analemma
Position der Sonne über ein Jahr hinweg.
Bahn der Sonne
[b]Aufgabe[/b][br][list][*]Verändere die Position der Sonne auf ihrem Weg von Osten nach Westen.[br][*]Klick mit der rechten Maustaste auf die Sonne und schalte die Animation ein.[br][*]Verändere das Datum und beobachte den Schatten im Lauf eines Jahres.[br][*]Wann ist Wintersonnenwende?[br][*]Blende die Schattenlinie und die Ekliptik mit der Himmelskugel ein.[br][/list][br] [br][i]Hinweis:[/i][br]Zum Berechnen des Sonnenstands eignet sich beispielsweise [url]http://www.sonnenverlauf.de/[/url][br]·
Andreas Lindner
Sonnenaufgang und Sonnenuntergang
Die Tabelle zeigt die Zeiten der Sonnenaufgänge und der Sonnenuntergänge im Jahr 2013 (Bad Ischl, Österreich).[br]Mit dem Befehl TrendSin[ <Liste>] kann eine Regressionskurve durch die Punkte gelegt werden.[br]Man sieht, dass der Tag mit dem spätesten Sonnenaufgang und dem frühesten Sonnenuntergang nicht zusammenfallen.[br][br][b]Aufgabe[/b][br]Beschreibt eine Sinuskurve den Verlauf von Sonnenauf- und Sonnenuntergang völlig korrekt?[br]Finde in diesem Modell die Tage mit kürzester und längster Sonnenscheindauer. Stimmen sie mit den gemessenen Daten (siehe Weblinks) überein?[br][br]Hinweis:[br]Daten zu Sonnenauf- und Sonnenuntergang finden sich beispielsweise auf[br]http://www.sunrise-and-sunset.com/de[br]http://www.zamg.ac.at/cms/de/klima/klimauebersichten/ephemeriden
Andreas Lindner
Sonne- und Mondfinsternis
Mit Animation und Text
Sonnensystem
Sonnensystem
Fluchtgeschwindigkeit
|
Die Bahn eines von der Erde abgeschossenen Körpers kann nur eine [b]Ellipse[/b], ein [b]Kreis[/b], eine [b]Parabel [/b]oder eine [b]Hyperbel [/b]sein. [b]Aufgabe[/b] Verändere die Abschussgeschwindigkeit v und beobachte, auf welcher Kurve der Körper sich bewegt. Zoome zum Abschussort hinein und blende die Kurve ein, die als Näherung auf Erdoberfläche verwendet werden kann. |
|
|
|
Andreas Lindner |
Earth (basic model)
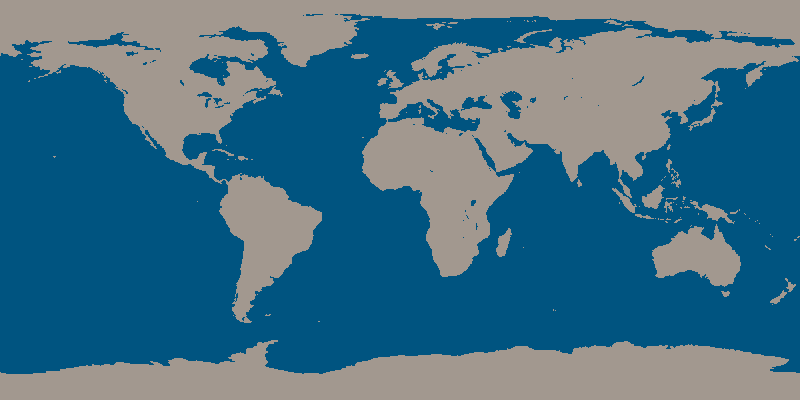
[color=#999999]This activity belongs to the [i]GeoGebra book[/i] [url=https://www.geogebra.org/m/uT3czZnE]Earth and Sun[/url].[/color][br][br][/color]Try wrapping a ball with wrapping paper, and you'll realize that due to its "curvature in all directions," there will always be spaces between the ball and the paper; achieving a perfect fit is impossible.To simplify, let's suppose the shape of the Earth is perfectly spherical. For the most faithful representation of the Earth, it's best to use a globe, because here, just like when wrapping a ball, any attempt to "flatten" the Earth's surface will always result in some kind of distortion, some kind of deviation from the correct measurements (whether distances, angles, or areas).This is because a sphere cannot be "unrolled," meaning its surface cannot be extended onto a plane. The following image corresponds to a world map. We recognize the outlines of the continents, but since it's a flat image rather than a spherical surface, we know it must necessarily be distorted. All world flat maps, in some way, "lie".
In this case, the spherical surface has been "painted" as if the Earth were a cylinder rolling on the paper (this method of projection is called cylindrical projection and, when applied to the Earth, is known as the Mercator projection). Notice that the Arctic (with its ice mass represented as a solid) and Antarctica appear extremely exaggerated, as both the North Pole and the South Pole stretch across the entire length of the image, instead of being represented as points.
For these reasons, it is advisable to have a globe template rather than relying on a world map, as shown in the following construction.[br][br][color=#999999]For better execution, it's recommended to download de GGB file.[/color]
[color=#999999]Author of the construction of GeoGebra: [color=#999999][url=https://www.geogebra.org/u/rafael]Rafael Losada[/url][/color][/color]
Erde, Sonne, Jahreszeiten
|
[b]Hinweise zur Bedienung:[/b] Einfaches Drehen geschieht bei Mausbewegung mit gedrückter rechter Maustaste. Verschieben der Ansicht mit Shift + linke Maustaste, mit einmaligem Linksklick wechselt man die Verschieberichtung (von x-y-Richtung zu y-Richtung) |
|
|