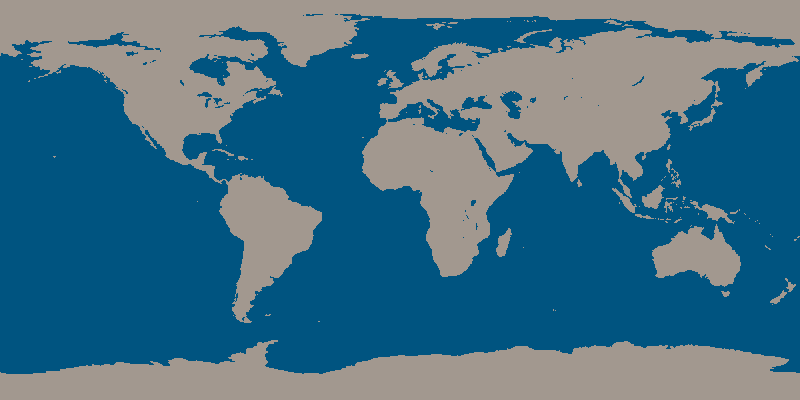
[color=#999999]This activity belongs to the [i]GeoGebra book[/i] [url=https://www.geogebra.org/m/uT3czZnE]Earth and Sun[/url].[/color][br][br][/color]Try wrapping a ball with wrapping paper, and you'll realize that due to its "curvature in all directions," there will always be spaces between the ball and the paper; achieving a perfect fit is impossible.To simplify, let's suppose the shape of the Earth is perfectly spherical. For the most faithful representation of the Earth, it's best to use a globe, because here, just like when wrapping a ball, any attempt to "flatten" the Earth's surface will always result in some kind of distortion, some kind of deviation from the correct measurements (whether distances, angles, or areas).This is because a sphere cannot be "unrolled," meaning its surface cannot be extended onto a plane. The following image corresponds to a world map. We recognize the outlines of the continents, but since it's a flat image rather than a spherical surface, we know it must necessarily be distorted. All world flat maps, in some way, "lie".

In this case, the spherical surface has been "painted" as if the Earth were a cylinder rolling on the paper (this method of projection is called cylindrical projection and, when applied to the Earth, is known as the Mercator projection). Notice that the Arctic (with its ice mass represented as a solid) and Antarctica appear extremely exaggerated, as both the North Pole and the South Pole stretch across the entire length of the image, instead of being represented as points.

For these reasons, it is advisable to have a globe template rather than relying on a world map, as shown in the following construction.[br][br][color=#999999]For better execution, it's recommended to download de GGB file.[/color]

[color=#999999]Author of the construction of GeoGebra: [color=#999999][url=https://www.geogebra.org/u/rafael]Rafael Losada[/url][/color][/color]