Correcaminos (bip, bip)
Se explica cómo realizar recorrer curvas y superficies con un punto de vista local.
Table of Contents
- Introducción
- Introducción
- Proyecciones
- Homotopía
- Triedro de Frenet
- Tubos
- Normal a una superficie
- 3D ZoomAcerca
- Cambio de vista
- Rectas
- Laberinto
- Poligonales
- Curvas
- Curvas
- Splines
- Superficies
- Cilindro
- Toro
- Toro (mapa de 7 colores)
- Esfera
- Moebius
- Moebius (mapa de 6 colores)
- Roman (Steiner)
- Silla de mono
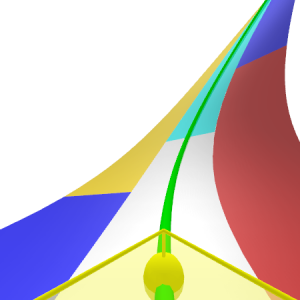
Introducción
[color=#999999]Esta actividad pertenece al libro de GeoGebra[i] [url=https://www.geogebra.org/m/pedzgbyt]Correcaminos (bip, bip)[/url][/i].[/color][br][br][right][i]Si la montaña no va a Mahoma, Mahoma irá a la montaña.[/i][/right]El objetivo principal de este libro GeoGebra es mostrar diversos modos de representar curvas y superficies, incluyendo un punto de vista local, como si estuviésemos navegando (surfeando) sobre la trayectoria.[br][br]Usar la vista 3D de GeoGebra para que muestre lo que vería un observador local, una cámara, que realizase un recorrido en el espacio entraña, en el momento de escribir esto, una dificultad fundamental. La vista 3D siempre muestra un paralelepípedo de aristas paralelas a los ejes cartesianos. No se puede definir un espacio ortoédrico arbitrario, sino que ha de establecerse un intervalo entre valores mínimos y máximos para cada coordenada. Esto significa que, de los infinitos rectángulos que comparten dos vértices opuestos dados, GeoGebra solo admite como base del escenario 3D el de aristas paralelas a los ejes. [br][br]Por ejemplo, no se puede establecer como escenario el paralelepípedo verde, de esquinas opuestas A(0, 0, 0) y B(3, 4, 1), y otro vértice en C(4, 2, 0). Al intentarlo, como muestra la siguiente construcción, lo que se crea es el ortoedro rojo, de esquinas opuestas A y B, pero con aristas paralelas a los ejes.[br][br]Para superar esta dificultad, optaremos por hacer caso al refrán arriba citado: dejar la cámara fija y trasladar dinámicamente la figura (curva o superficie) al frente de la cámara. Esto equivale matemáticamente (y físicamente, añadiría Galileo [url=https://es.wikipedia.org/wiki/Invarianza_galileana][img]https://www.geogebra.org/resource/scjbyz2p/0tuzuVw455vxurEw/material-scjbyz2p.png[/img][/url]) a cambiar el sistema de referencia. Además, haremos uso de cuatro conceptos: la proyección, la homotopía, el triedro de Frenet y el vector normal a una superficie en un punto dado.
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Laberinto
[color=#999999]Esta actividad pertenece al libro de GeoGebra[i] [url=https://www.geogebra.org/m/pedzgbyt]Correcaminos (bip, bip)[/url][/i].[/color][br][br]En esta construcción probamos la técnica de salir de un laberinto de modo automático, eligiendo siempre la pared derecha. El autómata (punto rojo) [b]no tiene ninguna información sobre la forma del laberinto[/b]. No existe ninguna trayectoria predefinida. Solo detecta si hay espacio libre a su derecha (en cuyo caso gira a la derecha para pegarse a la pared derecha) o si hay un obstáculo enfrente (en cuyo caso gira a la izquierda). Esta sencilla norma basta para no despegarse de su pared derecha y conseguir salir del laberinto. [br][br]En la construcción, pulsa el botón reproducir (en la esquina inferior izquierda del panel superior).[br][br][color=#cc0000]Nota: Para mejorar la agilidad de la ejecución, se recomienda [b]descargar [/b]el archivo GGB. Recordemos que, en tal caso, es probable que sea necesario [b]reajustar [/b]la altura de la vista 3D para recolocar el punto en la posición deseada. Para ese reajuste, puede ser de ayuda el deslizador magenta que aparece una vez descargado.[/color]
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Curvas
[color=#999999]Esta actividad pertenece al libro de GeoGebra[i] [url=https://www.geogebra.org/m/pedzgbyt]Correcaminos (bip, bip)[/url][/i].[/color][br][br]En esta construcción puedes ver un ejemplo con curvas. El botón [img]https://www.geogebra.org/resource/njceatrr/VDybceHABmIBMmu5/material-njceatrr.png[/img] te permite elegir entre algunas predefinidas:[br][list][*]Circunferencia[/*][*]Nudo de trébol[/*][*]Nudo de la abuela[br][/*][/list]También puedes elegir cualquier otra curva que quieras, siempre que conozcas una parametrización, activando la casilla Especifica.[br][br][color=#cc0000]Nota: Para mejorar la agilidad de la ejecución, se recomienda descargar el archivo GGB. Recordemos que, en tal caso, es probable que sea necesario reajustar la altura de la vista 3D para recolocar el punto en la posición deseada. Para ese reajuste, puede ser de ayuda el deslizador magenta que aparece una vez descargado (tal vez sea necesario ocultar temporalmente la vista gráfica 2 para verlo).[/color]
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Cilindro
[color=#999999]Esta actividad pertenece al libro de GeoGebra[i] [url=https://www.geogebra.org/m/pedzgbyt]Correcaminos (bip, bip)[/url][/i].[/color][br][br]En esta construcción puedes ver un ejemplo con superficies. El botón [img]https://www.geogebra.org/resource/njceatrr/VDybceHABmIBMmu5/material-njceatrr.png[/img] te permite elegir entre algunas trayectorias predefinidas:[br][list][*]La circunferencia (t, 0) [/*][*]El segmento (0, t)[/*][*]La hélice (t, t)[/*][*]El solenoide (5t, t)[/*][*]La elipse (t, sen(t))[br][/*][/list]También puedes elegir cualquier otro recorrido que quieras, siempre que conozcas una parametrización, activando la casilla Especifica.[br][br][color=#cc0000]Nota: Para mejorar la agilidad de la ejecución, se recomienda descargar el archivo GGB. Recordemos que, en tal caso, es probable que sea necesario reajustar la altura de la vista 3D para recolocar el punto en la posición deseada. Para ese reajuste, puede ser de ayuda el deslizador magenta que aparece una vez descargado (tal vez sea necesario ocultar temporalmente la vista gráfica 2 para verlo).[/color]
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]