Geometría plana. 1ºESO
Geometría plana
Table of Contents
- Polígonos. Clasificación y características.
- Polígonos y sus elementos
- Polígonos regulares anidados
- Polígonos engarzados
- Polígonos estrellados
- Ilusión óptica. Polígonos y circunferencias
- Áreas
- Unidad de área
- Polígonos en un geoplano, fijados los vértices (hasta 8 vértices)
- Área de Figuras Básicas
- 27 Áreas de los Polígonos
- Regular Pentagon: Area
- Regular Pentagon: Area (II)
- Problemas de Áreas
- Teorema de Pitágoras
- Teorema de Pitágoras. Demostración de Liu Hui
- Aplicaciones del teorema de pitagoras
- Teorema de Pitágoras. Problemas
- Perímetros
- Problemas de Perímetros
- Perímetro. Definición visual.
- Figuras circulares
- Perímetro de la circunferencia
- Circle Area (By Peeling!)
- Área de porciones circulares
- Problemas
- Cálculo de áreas de figuras compuestas
Polígonos y sus elementos
Un [b]polígono [/b]es una figura cerrada y plana que está limitada por segmentos consecutivos, que llamamos [b]lados[/b].[br][list][*]Los puntos donde se unen los lados se llaman [b]vértices[/b].[/*][*]Los segmentos que unen dos vértices (no consecutivos) se llaman [b]diagonales[/b].[/*][/list][b]Polígono regular[/b]: cuando todos sus lados y ángulos son iguales. Si no es regular, decimos que es irregular[br]El nombre del polígono es según su número de lados.[br][list][*]Polígono [b]convexo[/b]: si todos sus ángulos son convexos (menores de 180º)[/*][*]Polígono [b]cóncavo[/b]: cuando alguno de sus ángulos es cóncavo (más de 180º).[/*][/list]Los ángulos de todo triángulo suman 180º. Para cualquier otro polígono, podemos dividirlo en triángulos usando sus diagonales y usarlos para calcular la suma de sus ángulos. Por ejemplo, para un cuadrilátero la [br]suma es 360º, porque podemos dividirlo en 2 triángulos usando una diagonal.[br][br]Interactuando con la siguiente actividad podemos explorar y dibujar polígonos, y resolver ejercicios para comprobar si hemos aprendido los principales conceptos.
Ejercicios (instrucciones)
[list][*]Cuando haya varias preguntas, para que el ejercicio sea correcto deben estar todas bien.[/*][*]Los ejercicios correctos valen 1.5 puntos, pero los incorrectos penalizan también 1.5 puntos. Si se falla en las preguntas relativas a los elementos de los polígonos y la medida de los ángulos pero se tiene bien algún apartado, solo se penaliza con 1 punto.[/*][*]Podemos intentar tantas fichas como queramos. La actividad llevará la cuenta de las fichas correctas e intentadas.[/*][*]Se conservará la puntuación más alta alcanzada.[br][/*][/list]
[b]Cuestiones[/b][br][list=1][*]Siempre hay una [b]circunferencia circunscrita[/b] (que pasa por todos los vértices) para los polígonos regulares. La medida del [b]ángulo central[/b] está relacionada con la de los ángulos internos. ¿Sabrías decir cuál es la relación?[/*][*]¿Cuántas [b]diagonales[/b] hay en total en un polígono?[/*][*]¿Puede existir un triángulo cóncavo? ¿Y un cuadrilátero? [br][/*][*]Pon un ejemplo de: un cuadrilátero, un pentágono y un hexágono que sean cóncavos, y muestra cómo triangularlos para calcular la suma de sus ángulos[br][/*][*]¿Cuántos ángulos cóncavos puede tener un polígono? ¿Depende de su número de lados?[/*][*]Marca la casilla [b]Ejes de simetría[/b] e investiga cuántos ejes tienen los polígonos regulares (según el número de lados).[/*][*]Desmarcando la casilla "P. Regular", podemos mover los vértices, para crear otros polígonos. Haciendo clic en el punto, podemos moverlos usando los cursores. [br](Hazlo así si quieres investigar los ejes de simetría.)[br][/*][/list]
¿Comprobamos la suma de ángulos en papel?
[b]Triángulo[/b][list][*]Podemos dibujar un triángulo cualquiera en nuestro folio y repetir el dibujo que hace el applet para comprobar que la suma de ángulos es uno llano (180º).[/*][*]También podemos recortar los ángulos y luego componerlos juntos (en el lugar que asigna el applet), comprobando que, efectivamente, la suma de los tres es uno llano.[/*][/list][b]Cuadrilátero[/b][list][*]Dibujar un [b]cuadrilátero [/b]cualquiera.[/*][*]Recortamos los ángulos y los recomponemos situando uno junto a otro ¿completan el círculo (360º)? [br][/*][/list][br]Por ejemplo, podemos presentarlo así:
Creaciones de alumnos de 1ºESO de Marta López, del IES San Fernando de Badajoz.
Unidad de área
Teorema de Pitágoras. Demostración de Liu Hui
Problemas de Perímetros
Indicaciones
[list][*]Puedes cambiar la posición de las figuras[b] (1) y (2) [/b]moviendo los puntos rojos [color=#ff0000]x[/color][b].[/b][/*][*]Si la figura es demasiado grande o pequeña, puedes usar el deslizador con el dibujo de lupa para hacer zoom.[/*][*][b][/b]Cada ejercicio correcto vale [b]3.5 puntos[/b]. Los fallos no penalizan.[/*][*]La puntuación [b]máxima es 10 puntos[/b]. Al alcanzarla, el fondo de la pantalla pasará a ser [b][color=#6aa84f][b]verde[/b][/color].[br][/b][/*][/list]
Pistas
[color=#980000][1][/color] En el primer problema, recuerda que el rodapié no se pone en la zona de la puerta.[br][color=#980000][2][/color] En el segundo problema, se supone que la valla puede doblarse en forma circular, y la usaremos también para la puerta [color=#999999](por eso no nos dan sus datos)[/color]. Ten en cuenta que sólo puedes comprar un número entero de piezas.[br][list][*]Se indican todas las longitudes que necesitamos pero, [/*][*]cuando alguna se pueda comparar con las demás no se indicará su valor[br](por ejemplo si ya aparece esa medida, su doble o triple, pero trasladada o girada)[/*][/list][color=#980000][3][/color] En el tercer ejercicio, sólo se puede comprar un número entero de piezas. ¡Cuidado que el tamaño de las piezas viene en cm! [color=#666666]La puerta no afecta al friso (por eso no aparecen sus datos).[/color]
Grupos de bilingüe
Para traducir los enunciados a inglés:[br]Vocabulary: [br][color=#674ea7]rodapié[/color]: [i](UK)[/i] skirting-board, [i](US) [/i]baseboard.[br][color=#9900ff]valla[/color]: fence[br][color=#9900ff]pieza[/color]: piece[br][color=#9900ff]friso[/color]: frieze
Referencias
[size=85]Ilustración del [url=https://programacrea.educarex.es/]programa CREA[/url] (CC BY-SA).[/size]
Perímetro de la circunferencia
Cálculo de áreas de figuras compuestas
En los siguientes [b]ejercicios[/b], calcularemos áreas de figuras compuestas. Para resolverlos, tendremos que aplicar algún método de cálculo de áreas (ver más abajo), pues no habrá una única fórmula que nos proporcione la solución.[br]Por último, te mostraremos algunos casos aplicados ¡del siglo XVII!, con los planos para el cálculo de la superficie de la localidad de [url=https://es.wikipedia.org/wiki/Villamiel]Villamiel[/url], junto con una [b]tarea[/b] relacionada, y otro con la ciudad de Badajoz.[br][br]Si quieres practicar primero con figuras simples, puedes probar con [url=https://www.geogebra.org/m/BtcGZuqa]esta otra actividad (clic aquí)[/url].
Instrucciones
[list][*]Puedes mover el centro (marcado con "x"), para ver mejor la figura.[/*][*]Cada respuesta correcta vale 2.5 puntos, y cada fallo resta 1 punto.[/*][*]La puntuación máxima es 10. Al alcanzarla, el fondo de la pantalla pasará a ser [color=#6aa84f][b]verde[/b][/color].[/*][*]Pulsa el botón "corregir" para comprobar si has hecho bien la figura.[/*][*]Redondea con 2 decimales.[/*][/list]
Métodos de cálculo de áreas
Está claro que no es posible tener una fórmula para el cálculo del área de cada figura.[br]Sin embargo, conociendo algunos métodos, no es necesario que recordemos muchas. [br][list][*]De hecho, la manera de deducir el área de un polígono regular, o de un trapecio se basan en estos métodos. [/*][*]Concretamente, en el de [b]descomposición de áreas[/b].[/*][*]Podemos dividir la figura en otras más pequeñas para las que sí conozcamos la fórmula.[br][list][*]Normalmente, se trata de sumar esas áreas más pequeñas, aunque[/*][*]a veces puede resultar útil pensar que lo que se ha hecho es "recortar" una figura pequeña a una figura mayor, para la cual también tenemos fórmula de su área.[br][/*][/list][/*][/list]
La superficie de Villamiel
Como curiosidad, mostramos esta imagen de un grabado de 1660, donde se utilizan las matemáticas y, en particular, el método de descomposición de áreas, para representar y calcular de la superficie de [url=https://es.wikipedia.org/wiki/Villamiel_de_Toledo]Villamiel[/url] de Toledo. [br]En este caso, la planta se ha reducido a 48 figuras geométricas.
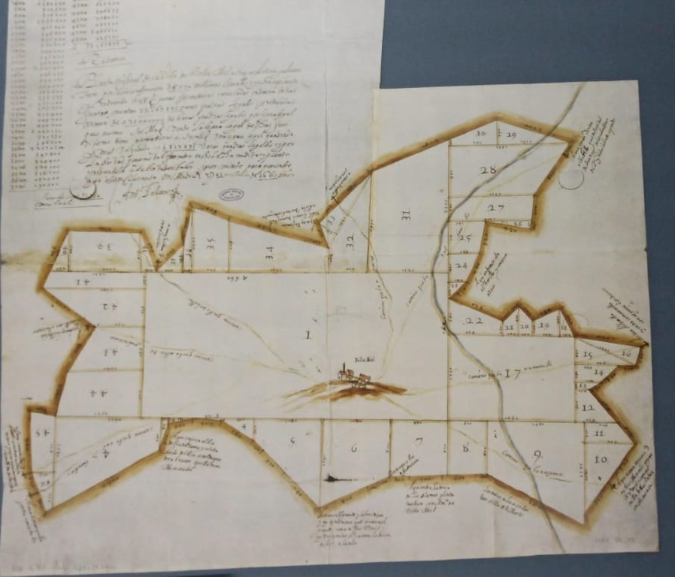
Planos para el cálculo de la superficie de Villamiel, en 1660. Exposición del Archivo General de Simancas.
Tarea 1. Analizando el plano
Como se ve en la figura, para calcular la superficie de este terreno, dividieron el recinto amurallado en 48 parcelas para las cuales sí podían calcular el área aplicando una fórmula conocida. [br]Usaron las longitudes que sí podían medir sobre el terreno o en el mapa, usando proporcionalidad geométrica (la escala del mapa).[br][br]Ahora es [b]nuestro turno[/b] para hacer un pequeño análisis de estas figuras. Puedes elegir el plano anterior de Villamiel o elegir alguno similar de estos [url=https://www.mcu.es/ccbae/es/consulta/resultados_navegacion.do?busq_sobreautoridades=BAA20160058697&descrip_sobreautoridades=Obras%20sobre%20este%20tema:%20Planos%20catastrales-#[#BAA20060371421##]planos catastrales del S.XVII (archivo de Simancas)[/url] [también está el de Villamiel, por si se necesita con más resolución].[br]Se trata de, bien en forma de [b]tabla [/b]o en forma de [b]lista[/b], clasificar [br][list][*]cuáles han utilizado y [/*][*]cuántas hay de cada tipo. [br][list][*]Indicaremos los números de parcela de cada tipo[/*][*]también pondremos cuántas son en total.[/*][*]Por supuesto, la suma de todas deberá ser las 48 parcelas.[br][/*][/list][/*][*]Haremos un dibujo esquemático de este tipo de figura. [br]Como curiosidad, fíjate en que casi ninguno de los trapecios rectángulos está apoyado en sus bases.[/*][*]Pondremos la fórmula que nos permite calcular su área.[br][/*][/list]Puedes hacerlo en tu libreta, o bien en el espacio que proporcionamos a continuación.[br]
Tarea 2. Nuestro turno
Por último, es nuestro turno de hacer un plano como el de Villamiel, para el que calcularemos su superficie.[br][list=1][*]Podemos elegir nuestra "villa": pueblo, ciudad, o una localidad que nos guste, y hacer su plano aproximado.[br][list][*]También podemos buscarlo en internet,[/*][*]o bien hacer uno enteramente de nuestra invención... pero que se ajuste a la estructura de una ciudad de, por ejemplo, el siglo XVII.[/*][*]¡Pero ten cuidado de poner medidas que sean razonables![br][/*][/list][/*][*]Puedes hacer una simplificación del plano para que no salgan tantas parcelas como en el caso de Villamiel.[/*][*]Tendrás que proponer una descomposición en figuras simples para el cálculo del área.[br][list][*]Toma como ejemplo el plano de Villamiel, procurando usar figuras grandes, para no tener que hacer muchos cálculos.[br][/*][/list][/*][*]Ojo al hacer la simplificación del plano: deben aparecer al menos tres formas geométricas diferentes en la descomposición en figuras simples.[/*][*]Efectúa los correspondientes cálculos de áreas y deja todo apuntado en tu libreta, junto con [br][list][*]el dibujo que hayas hecho de tu "villa",[/*][*]las medidas tomadas[br][/*][*]las áreas parciales[/*][*]el área total de la villa.[br][/*][/list][/*][*]Como siguiente apartado, incluye también el perímetro del recinto amurallado (o de la población, si no has dibujado muralla).[br][list][*]No es necesario que hagas el cálculo exacto de lados inclinados u otras longitudes que te falten (utilizando el teorema de Pitágoras o similar). [/*][*]Puedes medir en tu plano con la regla y, por proporcionalidad (el plano está a escala), calcular qué longitud le corresponde en la realidad.[/*][/list][/*][/list]Muestra la libreta con tu trabajo a tu profesor/a, o incluye aquí la redacción de la solución, junto con el enlace al dibujo de tu "villa".
Reto computacional. Utilizamos GeoGebra
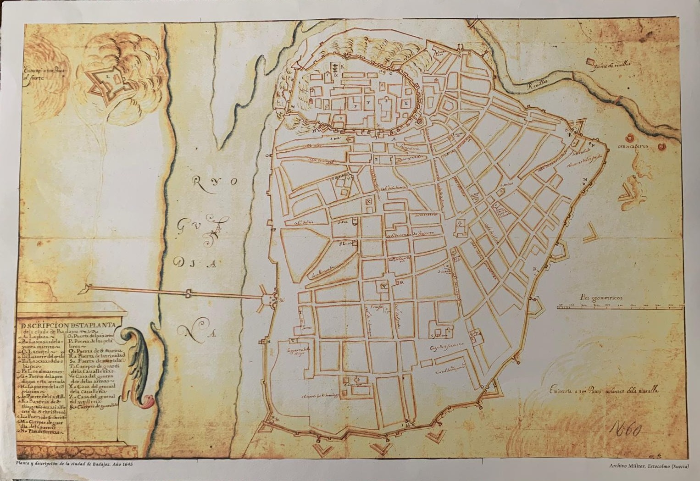
Sánchez, C. y Sánchez R. (2003). Badajoz en el Krigsarkivet. El hallazgo de la visión más lejana. Ayuntamiento de Badajoz, via Lorenzo Blanco Nieto
Reto computacional. Utilizamos GeoGebra
Vamos a hacer un análisis similar al anterior, para el plano de Badajoz en 1645 que tenemos aquí arriba.[br]Para ello, utilizaremos GeoGebra, donde [br][list=1][*]Descargamos la fotografía del plano que hay sobre estas líneas y la subimos como imagen a GeoGebra.[/*][*]Trazamos el contorno como un polígono con muchísimos puntos (fíjate en el "resultado esperado" que se incluye más abajo). [br][list][*]Podemos simplificarlo un poco, para que la figura no sea tan compleja.[/*][*]Por cierto ¿qué nombre tendrá ese polígono con tantos lados?[/*][/list][/*][*]Descomponemos el área de la ciudad en otros polígonos más pequeños, de los que sabríamos calcular su área, aunque en este caso usaremos GeoGebra para calcularla. [br][list][*]Por ejemplo, rectángulos, triángulos y trapecios.[/*][*]Se admiten pequeñas trampas, como mover un poco los puntos para que los trapecios cuadren mejor (en el "resultado esperado" lo hemos hecho así).[/*][*]También podemos quitar los baluartes (esos salientes defensivos pentagonales).[/*][/list][/*][*]Observamos las áreas que calcula GeoGebra para la figura completa y para cada una de las partes. Comprobamos que la suma de las partes es, efectivamente, el área de la figura grande.[/*][*]En el mapa se aprecia una escala, pero no se lee demasiado bien. Está expresada en pies geométricos. Un pie geométrico equivale a 0.3048 metros. [br][list][*]Establecemos una escala "a ojo", pero que sea más o menos realista. Ten en cuenta que el puente sobre el Guadiana mide unos 585m.[/*][*]Comprobamos con GeoGebra que la escala que has elegido hace que esa medida sea aproximadamente correcta.[/*][/list][/*][*]Utilizamos esta escala para calcular el área de la superficie amurallada de Badajoz en 1645. ¿Por cuánto hay que multiplicar el número que ofrece GeoGebra?[/*][/list]A continuación tenemos un ejemplo de la descomposición que se espera que hagamos. Por supuesto, hay muchas descomposiciones posibles. Lo que más nos interesa es utilizar la menor cantidad de polígonos, para no tener que hacer tantos cálculos.