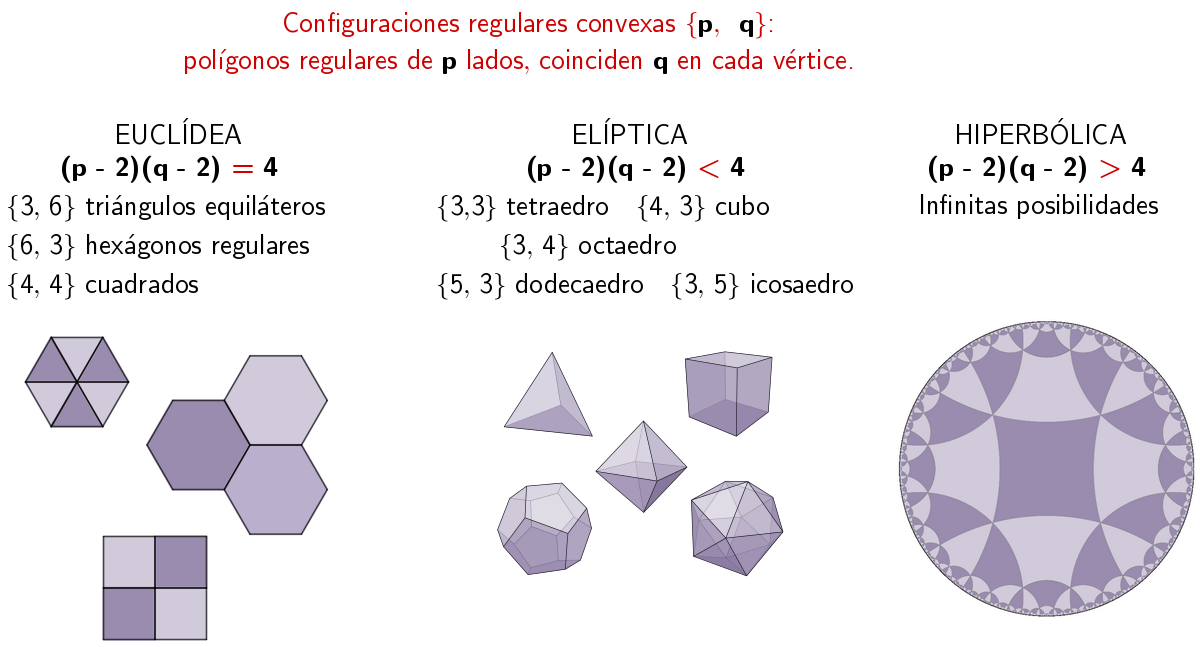
Teselaciones regulares
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra [/i][url=https://www.geogebra.org/m/vuuufnr8]Teselados regulares euclídeos, elípticos e hiperbólicos[/url].[/color][br][br]Una teselación regular {[i]p[/i], [i]q[/i]} es una teselación de polígonos regulares de [i]p[/i] lados donde [i]q[/i] se encuentran en cada vértice. [br][br]Veremos que la relación entre [i]p[/i] y [i]q[/i] depende de la geometría que consideremos.[br][br]El ángulo interior de un polígono regular de [i]p[/i] lados mide [math]\pi-\frac{2\pi}{p}[/math]. Como en cada vértice concurren [i]q[/i] de ellos, la suma total, [math]q\left(\pi-\frac{2\pi}{p}\right)[/math] ha de ser:[br][list][*]igual a [math]2\pi[/math] (geometría euclídea, la suma de los ángulos de un triángulo es igual a [math]\pi[/math]), [/*][*]menor que [math]2\pi[/math] (geometría elíptica, la suma de los ángulos de un triángulo es mayor que [math]\pi[/math]), o[/*][*]mayor que [math]2\pi[/math] (geometría hiperbólica, la suma de los ángulos de un triángulo es menor que [math]\pi[/math]). [/*][/list]Transformando esa expresión, tenemos:[br][list][*]En la geometría euclídea, se cumple que ([b][/b][i]p[/i] - 2) ([b][/b][i]q[/i][b][/b] - 2) = 4. Solo hay 3 casos posibles.[/*][*]En la geometría elíptica, se cumple que ([i]p[/i] - 2) ([i]q[/i] - 2) < 4. Solo hay 5 casos posibles.[/*][*]En la geometría hiperbólica, se cumple que ([i]p[/i] - 2) ([i]q[/i] - 2) > 4. Hay infinitos casos posibles.[/*][/list]Nota: en esta clasificación, y en este libro, suponemos que los polígonos de la teselación regular tienen al menos 3 lados. En la geometría elíptica pueden darse [url=https://es.wikipedia.org/wiki/Poliedro_esf%C3%A9rico#Casos_impropios]teselaciones con polígonos de 2 lados (¡incluso solo 1!)[/url].

Observa que en las geometrías euclídea e hiperbólica, el número de regiones poligonales es infinito, mientras que en la geometría euclídea es finito. Escher, que tenía como uno de sus objetivos la representación visual de los procesos infinitos, expresaba este hecho con estas palabras (referidas a la esfera con peces de la imagen inferior):[br][br][i]Si giras esta esfera entre las manos, aparecen peces tras peces en una sucesión interminable. Aunque son limitados en número, simbolizan la idea de infinitud de una manera que no se puede lograr con una superficie plana.[/i]

[size=85]M.C. Escher, [i]Fish[/i], teselación esférica, grabado en madera.[/size]
[color=#999999]Autor de la actividad: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]