"EL TEOREMA DE PITÁGORAS EN COLOR, PAPEL Y BITS"
Que el alumno descubra la relación entre los lados del triangulo (en especial del rectángulo), en ambientes híbridos de aprendizaje y concluya en la formulación del Teorema de Pitágoras, por medio de los ecosistemas educativos híbridos se busque propongan actividades que empleen diversos recursos y estrategias para la enseñanza y aprendizaje del famoso teorema (de Pitágoras).
Table of Contents
- Actividad 00: INTRODUCCIÓN
- ACTIVIDAD 00: INTRODUCCION
- Actividad 01: RECONOCIENDO TRIÁNGULOS Y CUADRADOS
- ACTIVIDAD No. 1
- Actividad 02: EL GEOPLANO
- Actividad 02: El Geoplano
- Actividad 02a: El Geoplano
- Actividad 02b: El Geoplano
- Actividad 02c: El Geoplano
- Actividad 02d: El Geoplano
- Actividad 02e: El Geoplano
- Actividad 03: NUEVOS TÉRMINOS Y SUS RELACIONES EN EL TRIÁNGULO RECTÁNGULO.
- Actividad 03
- Actividad 04: EL TRIANGULO Y LOS CUADRADOS DE SUS LADOS
- Actividad 04: Relación de TRIÁNGULOS y CUADRADOS en el geoplano
- Actividad 04a: Relación de TRIÁNGULOS y CUADRADOS en el geoplano
- Actividad 04b: Relación de TRIÁNGULOS y CUADRADOS en el geoplano
- Actividad 04c: Relación de TRIÁNGULOS y CUADRADOS en el geoplano
- Actividad 04d: Relación de TRIÁNGULOS y CUADRADOS en el geoplano
- Actividad 05: PITÁGORAS Y LOS PITAGÓRICOS
- Un poco de Pitágoras
- Actividad 06: OTRAS DEMOSTRACIONES
- Otro tipo de demostraciones
- Actividad 07: TERNAS PITAGÓRICAS
- Ternas Pitagóricas
- Actividad 08: LAS LUNAS DE HIPÓCRATES
- Las lunas de Hipócrates
- Actividad 09: APLICACIONES
- Actividad 09a: APLICACIONES
- Actividad 09b: APLICACIONES
- Actividad 09c: APLICACIONES
ACTIVIDAD 00: INTRODUCCION
[justify]La matemática forma parte de nuestra vida desde que entramos al sistema educativo: preescolar, primaria, secundaria, preparatoria. En estos trece años, los conceptos se abordan varias veces aumentando, paulatinamente, el nivel de complejidad. El objetivo es obtener un entendimiento cada vez más profundo y consolidado.[br][br] Se eligió centrar la atención en el Teorema de Pitágoras (TP) porque se ha identificado como el teorema individual más estudiado de la matemática, por lo que en las aulas prevalece una visión simplista de este conocimiento matemático, que no permite ver cómo el TP se integra en una red estructurada de ideas que abarca diferentes áreas de la disciplina, entre las que se destacan la teoría de números, el álgebra, la trigonometría, la geometría analítica o el cálculo.[br][br] En el caso del TP, un primer contacto con el concepto se presenta en el tercer año de año de secundaria (en ocasiones en segundo año), con actividades que casi siempre se refieren al cálculo de los lados de un triángulo rectángulo, donde toman una generalización del TP, expresándose como si fuera única (la relación Pitagórica). Esto es un reflejo reduccionista de las creencias de los profesores, que constituyen la directriz de la elección de las actividades que proponen a sus estudiantes, a pesar que cuentan con lineamientos pedagógicos plasmados en los programas de estudio y los libros de texto. [/justify][justify][/justify][br]
ACTIVIDAD No. 1
1 Recordando triángulos y cuadrados.
1.1 Traza en tu libreta los diversos triángulos que conoces y escribe su nombre a cada uno de ellos, junto con sus características.
1.2 Observa la aplicación y recuerda los diversos tipos de ángulos.
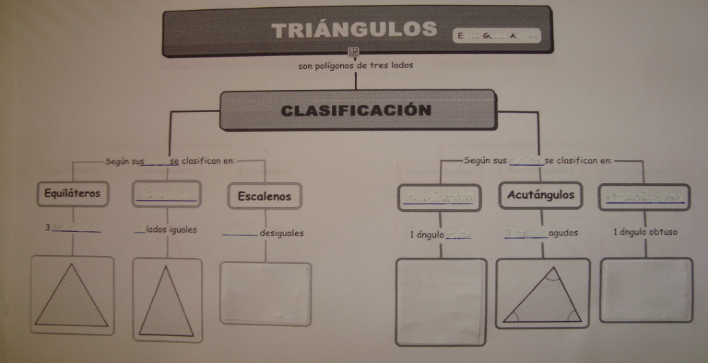
1.3 Observa y analiza la clasificación de los triángulos según sus ángulos.
1.4 Complementa el formato recibido, marca los lados de cada triángulo con color azul y señala los ángulos de cada triángulo con color rojo.
Recuerda las características del cuadrado.
1.5 Enlista las características del cuadrado y traza uno en tu libreta.
Actividad 02: El Geoplano
[b]¿Qué es el geoplano?[br][br][/b]El geoplano es un elemento didáctico manipulable que ayuda a introducir y afianzar gran parte de los conceptos de la geometría plana, al ser una herramienta física permite a los estudiantes obtener una mayor comprensión de diversos conceptos de las matemáticas, mediante el geoplano: [br][list][*]Se pueden formar figuras geométricas.[/*][/list][list][*]Los estudiantes puedan establecer semejanzas y diferencias entre paralelismo y perpendicularidad.[/*][/list][list][*]Identifica la relación entre superficie-volumen.[/*][*]Entre muchos otros conceptos[/*][/list]Esta herramienta es una superficie con forma de figura geométrica, cuadrados, rectángulos, círculos, elipses, etc., donde su superficie esta una malla cuadrangular en que los puntos de intersección de la malla se coloca un poste
imagen 00
Para trabajar en el geoplano haremos uso de ligas, de preferencia de colores, las cuales describirán las figuras a desarrollar.[br][b]ACTIVIDAD 01.-[/b] toma una liga y en momentos diferentes[br][list][*]Desarrolla un cuadrado, donde uno de sus lados sea horizontal respecto al geoplano.[br][/*][*]Desarrolla un rectángulo, donde uno de sus lados sea horizontal respecto al geoplano.[br][/*][/list]
imagen 01
[b]ACTIVIDAD 02.-[/b] toma una liga y desarrolla en diferentes momentos[br][list][*]Un triangulo acutángulo, donde uno de sus lados sea paralela respecto al geoplano.[/*][/list][list][*]Un triangulo rectángulo, donde uno de sus lados sea paralela respecto al geoplano.[/*][*]Un triangulo obtusángulo, donde uno de sus lados sea paralela respecto al geoplano.[/*][/list]Comprueba que cada figura que realices cumpla con las características correspondientes de cada tipo de triángulo
imagen 02
Actividad 03
3.1 De acuerdo a lo elaborado en los capítulos anteriores, traza en tu libreta tres triángulos, uno acutángulo, otro rectángulo y otro obtusángulo.
3.2 A cada lado de cada triángulo, traza su cuadrado (área cuadrada), puedes trazarlo con lápiz o elaborarlos con hojas de color.
3.3 Rellena con el granulado sólo las áreas de los dos cuadrados trazados a los lados de cada triángulo. Una vez, llenados esos cuadrados, traslada su contenido hacia el cuadrado trazado sobre la diagonal del triángulo.
3.4 Escribe en tu libreta las relaciones que observaste y que concluyes al realizar la actividad con cada uno de los triángulos.[br]- En en triángulo acutángulo....[br]- En el triángulo rectángulo...[br]- En el triángulo obtusángulo...
Actividad 04: Relación de TRIÁNGULOS y CUADRADOS en el geoplano
[br][br]Recordemos algunos conceptos del triángulo que necesitaremos[br][br][br]
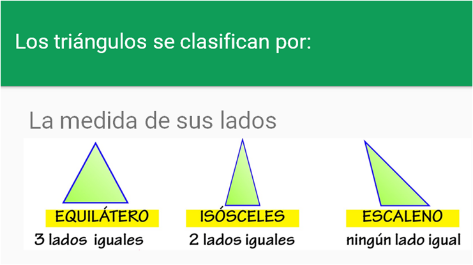
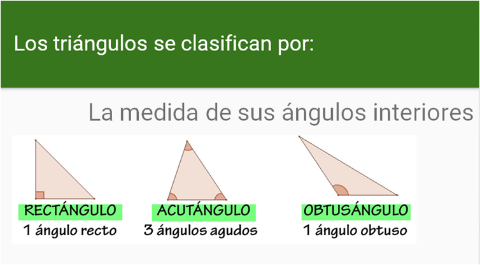
Dada esta última clasificación de triángulos[br][br][b][size=150][justify]LA RELACIÓN QUE HAY ENTRE LA CLASIFICACIÓN DE UN TRIANGULO CON RESPECTO A SUS ÁNGULOS INTERIORES Y LAS ÁREAS DE LOS CUADRADOS EN BASE A LOS LADOS DEL TRIÁNGULO [br][/justify][/size][/b][br]Dado un triángulo
Construye los cuadrados en base a la los lados del triángulo que ya tienes[br]Ten en cuenta que es un cuadrado por lado
Estima el área de los cuadrados obtenidos y anótalas en tu libreta
Un poco de Pitágoras
A continuación escucharás y observarás un vídeo acerca de Pitágoras y los Pitagóricos.
Pon a prueba lo que aprendiste a partir del vídeo.
Selecciona la respuesta correcta:
1. ¿Quién descubrió el Teorema de Pitágoras?
2. ¿Dónde nació Pitágoras?
3. ¿Cuál es la técnica que utilizaban los egipcios para el trazo de ángulos rectos?
4. Hablaban sobre temas religiosos, filosofía y matemáticas. Tenía 600 adeptos aproximadamente esta sociedad.
5. ¿Cuáles son las principales aportaciones de la escuela Pitagórica ?
6. Características de la sociedad fundada por Pitágoras
7. Principales descubrimientos y atribuciones de los Pitagóricos a los números:
8. Principales ideas y teorías de los Pitagóricos sobre el universo:
9. ¿Cuál era el símbolo de los pitagóricos?
10. En el símbolo de los Pitagóricos se encuentra la demostración de los números que ellos mismos se negaban a reconocer, ¿Cuáles son estos números?
Otro tipo de demostraciones
Observa otros demostraciones de Pitágoras:
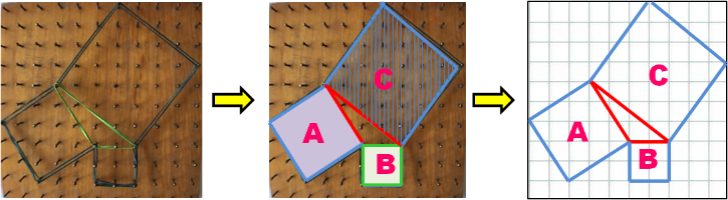
[color=#0000ff]Explica con palabras cómo es que se comprueba en la figura anterior el Teorema de Pitágoras:[/color]
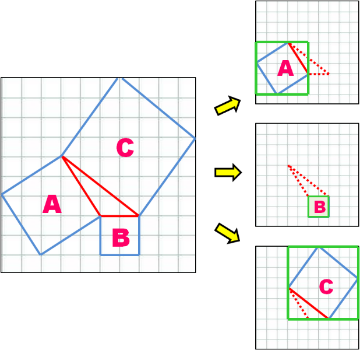
[color=#0000ff]Explica con palabras cómo es que se comprueba el teorema de Pitágoras en la animación anterior:[/color]
[color=#0000ff]Explica con palabras cómo se comprueba el Teorema de Pitágoras en la animación anterior:[/color]
Anota tus conclusiones de la sesión:
[color=#0000ff]¿Qué aprendí?[/color]
[color=#0000ff]¿Cómo lo aprendí?[/color]
[color=#0000ff]Ejemplos y preguntas:[/color]
Ternas Pitagóricas
Como viste en el vídeo anterior, los egipcios utilizaban una cuerda dividida en partes iguales con 3,4 y 5 nudos con los que formaban un triángulo rectángulo el cual les permitía marcar campos, medir la tierra y trazar ángulos rectos.
Una [b]tripleta pitagórica[/b] o [b]terna pitágorica [/b]es una colección de números enteros positivos que satisfacen el teorema de Pitágoras.[br]La terna pitagórica [size=200](3,4,5) [size=100]también conduce a [/size][/size][size=200](6,8,10)[/size][size=200][size=100], [/size][/size][size=200](9,12,15)[/size][size=200][size=100], [/size][/size][size=200](12,16,20)[/size][size=200][size=100], [/size][/size][size=200](5,20,25)[/size][size=200][size=100]...[/size][/size]
La terna pitagórica [size=200](3,4,5)[/size] se llama [b]básica[/b] o [b]primitiva[/b] porque a partir de ella se generan otras más.
[color=#0000ff]1. Explica cómo es que se generaron las demás ternas a partir de la tripleta primitiva (3,4,5)[/color]
Los babilonios elaboraron la primera relación de ternas pitagóricas de la que se tenga conocimiento, se encuentra en la tablilla Plimpton 322 de hace 1800 años a. C.
Los babilonios pudieron generar ternas o tripletas pitagóricas a partir de dos números enteros y se cree que lo hicieron con las siguientes fórmulas, cuando p y q son números naturales y p>q:[br][b]2pq[/b] para la longitud de un cateto[br][b]p[sup]2[/sup]-q[sup]2[/sup][/b] para la longitud del otro cateto[br][b]p[sup]2[/sup]+q[sup]2[/sup][/b] para la longitud de la hipotenusa[br]
Observa y comprueba como se generan ternas pitagóricas con las fórmulas anteriores:
A continuación se muestran las 10 primeras ternas primitivas, es decir aquellas que no se generan a partir de otras ternas.[table][tr][td]3,4,5[/td][td]11,60, 61[/td][/tr][tr][td]5,12,13[/td][td]12,35,37[/td][/tr][tr][td]7,24,25[/td][td]13,84,85[/td][/tr][tr][td]8,15,17[/td][td]15,112,113[/td][/tr][tr][td]9,40,41[/td][td]16,63,65[/td][/tr][/table]
[color=#0000ff]2. ¿Qué relación o propiedades encuentras entre los números de cada una de las ternas? ¿qué tipo de números son?[/color]
Ahora observa las siguientes ternas que se generan a partir de otras:[br][table][tr][td]6,8,10[/td][td][/td][/tr][tr][td]10,24,26[/td][td][/td][/tr][tr][td]16,30,34[/td][td][/td][/tr][tr][td]12,16,20[/td][td][/td][/tr][tr][td][/td][td][/td][/tr][/table]
[color=#0000ff]3. ¿Qué relación o propiedades encuentras entre los números de cada una de las ternas? ¿qué tipo de números son?[/color]
Para finalizar, completa:[br]
[color=#0000ff]Propiedades [br]5. Se puede observar que una tripleta o terna pitagórica tiene:[/color]
[color=#0000ff]6. ¿Para qué consideras que te sirva el manejo y generar ternas pitagóricas?[/color]
Las lunas de Hipócrates
Usa el siguiente tablero para realizar lo siguiente:
[br]
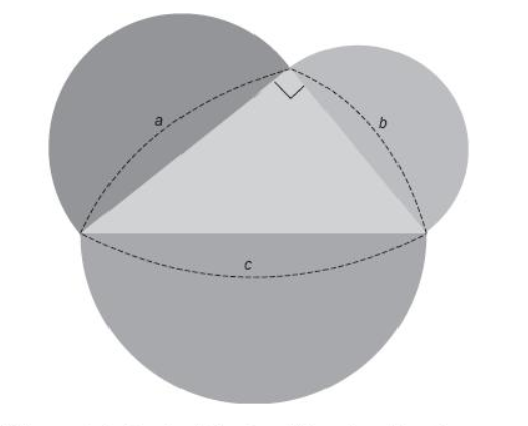
1. Instala una cerca de cartón alrededor de los tres semicírculos.[br]2. Instala una cerca triangular alrededor del triángulo central.[br]3. Vacía frijoles de goma o de chocolate en los semicírculos. Asegúrate que los frijoles llenen completamente los semicírculos sin que se encimen y que tampoco queden huecos grandes.[br]4. Retira la cerca del triángulo central.[br]5. Inclina el tablero para que los frijoles se deslicen hacia el semicírculo construido sobre la hipotenusa.[br]6. Coloca la cerca triangular en su lugar.[br]7. Comprueba que los frijoles llenen completamente el semicírculo más grande.[br]
[color=#0000ff]1. ¿Qué puedes decir acerca de la suma de las áreas de los semicírculos construidos sobre los catetos del triángulo rectángulo comparada con el área del semicírculo construido sobre la hipotenusa? [br]Expresa tu hallazgo con palabras.[/color]
Ahora, vas a escribir expresiones algebraicas para las áreas de los semicírculos y sus relaciones.
El diámetro de cada semicírculo es congruente con el lado correspondiente del triángulo. ¿Cuál es el radio de cada uno de los semicírculos sobre los lados del triángulo rectángulo? [color=#0000ff][br]1. Escribe el radio del semicírculo sobre el lado [i]a[/i][/color]
[color=#0000ff]2. Radio del semicírculo sobre el lado [i]b[/i][/color]
[color=#0000ff]3. Radio del semicírculo sobre el lado [i]c[/i][/color]
[color=#0000ff]4. ¿Cuál es el área del círculo de radio [img]http://www.scielo.org.mx/img/revistas/ed/v20n1/a6e1.jpg[/img]?[/color]
[color=#0000ff]5. ¿Cuál es el área de un semicírculo de radio [img]http://www.scielo.org.mx/img/revistas/ed/v20n1/a6e1.jpg[/img]?[/color]
[color=#0000ff]6.[/color] [color=#0000ff]Escribe una expresión algebraica para cada una de las áreas de los semicírculos. Área del semicírculo sobre el lado [i]a[/i][/color]
[color=#0000ff]7.[/color] [color=#0000ff]Escribe una expresión algebraica para cada una de las áreas de los semicírculos. Área del semicírculo sobre el lado [i]a[/i][/color]
[color=#0000ff]8. Escribe el área del semicírculo sobre el lado [i]b[/i][/color]
[color=#0000ff]9. Escribe el área del semicírculo sobre el lado [i]c[/i][/color]
[color=#0000ff]10. Usa notación algebraica para expresar la suma de las áreas de los dos semicírculos de radios [img]http://www.scielo.org.mx/img/revistas/ed/v20n1/a6e2.jpg[/img][/color]
[color=#0000ff]11. Utiliza notación algebraica para expresar que la suma de las áreas de los semicírculos sobre los catetos [i]a[/i] y [i]b[/i] del triángulo rectángulo es igual al área del semicírculo sobre la hipotenusa [i]c[/i][/color]
[color=#0000ff]12. Factoriza y simplifica ambos lados de la ecuación [img]http://www.scielo.org.mx/img/revistas/ed/v20n1/a6e3.jpg[/img] para mostrar que es equivalente a la ecuación [i]a[sup]2[/sup] + b[sup]2[/sup] = c[sup]2[/sup].[/i][/color]
[color=#0000ff]13. Puedes hacer esto en varios pasos. Puedes, por ejemplo, multiplicar ambos lados por 2 y dividir ambos lados entre [b]π[/b]. Escribe la ecuación simplificada:[/color]
[color=#0000ff]14. Ahora puedes expandir los términos cuadrados. Escribe la ecuación correspondiente:[/color]
[color=#0000ff]15. Finalmente puedes multiplicar ambos lados por 4[/color]
[color=#0000ff]16. Verifica que puedes invertir todos los pasos. Esto es, empieza con la ecuación [i]a[sup]2[/sup] + b[sup]2[/sup] = c[sup]2[/sup] y[/i] muestra paso a paso que, a partir de esta relación, puedes obtener la relación entre los semicírculos.[br][img]http://www.scielo.org.mx/img/revistas/ed/v20n1/a6e4.jpg[/img][/color][br]
Observa la siguiente animación:
Mueve los puntos. Cambia de tamaño el triángulo rectángulo, mueve los puntos, forma polígonos distintos, cóncavos y convexos, y contesta:[br][color=#0000ff]1.¿Qué sucede con las áreas de los polígonos?[br][/color][br]
[color=#0000ff]2.¿Se cumple el teorema de Pitágoras? Demuestrálo.[/color]
[color=#0000ff]3. Escribe una regla general para el teorema de Pitágoras.[/color]
Actividad 09a: APLICACIONES
[center][b]GUÍA DE PROBLEMAS Y EJERCICIOS DE APLICACIÓN DEL TEOREMA DE PITÁGORAS[/b][br][b][/b][b]Problemas De Aplicación[/b][br][/center][br]
[color=#0000ff][b]1) [/b][size=150] Traza en un geoplano el cuadrilátero mostrado en la figura y estima su perímetro y su superficie[/size][/color]
[color=#0000ff][b][size=150]2) [/size][/b][size=150] Un maestro albañil desea trazar las guías para la cimentación de una obra, debe trazar una esquina con un ángulo recto y solo cuenta con una cuerda de 6 m de largo. Describe lo que podría hacer el maestro para realizar su trabajo.[br][/size][/color][br][br]
