[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra [/i][url=https://www.geogebra.org/m/vuuufnr8]Teselados regulares euclídeos, elípticos e hiperbólicos[/url].[/color][br][br]Una de las ideas más atractivas para la mente humana es la idea de la supresión de barreras, de límites. La infinitud. La eternidad. El arte islámico supo aprovechar las "teóricamente" infinitas copias de un mismo motivo geométrico para recrear esa idea en quienes transiten entre sus mosaicos.[br][br]Este libro de GeoGebra pretende crear una fábrica de [b]teselaciones regulares[/b]. Es una continuación de [url=https://www.geogebra.org/m/fwpemasd]La fábrica de teselados[/url], pero por un lado restringida a los azulejos que son polígonos regulares y por otro lado ampliada, siguiendo los pasos del genial artista [url=https://es.wikipedia.org/wiki/M._C._Escher]M.C. Escher[/url], a las geometrías elíptica e hiperbólica. [br][br]Las actividades aquí recogidas pueden servir como base para la [b]propuesta de proyectos educativos[/b], ya que permite observar, explorar, conjeturar, comprobar e investigar una amplia gama de situaciones matemáticas, al tiempo que estimula el sentido estético. La exploración de geometrías diferentes a la euclídea permite apreciar sus diferencias y semejanzas.[br][br]Para la exploración de la geometría elíptica elegiremos el más sencillo de los modelos: la esfera. Para la geometría hiperbólica hemos elegido, tanto por su aspecto estético como por ser "abarcable" con la vista, el modelo del disco de Poincaré.[br][br]Consideraremos también el aspecto topológico, en forma de grafo dual asociado a cada teselación. Si no estás familiarizado con ellos, puedes ver una introducción en mi libro de GeoGebra [url=https://www.geogebra.org/m/yybrap57]Redes y Grafos[/url].[br][br]Además de recoger los distintos teselados regulares que se pueden generar, en este libro de GeoGebra he escogido el siguiente mosaico cuadrado del Palacio Nacional de Sintra (Portugal) para ser representado en las tres geometrías: euclídea, elíptica e hiperbólica.

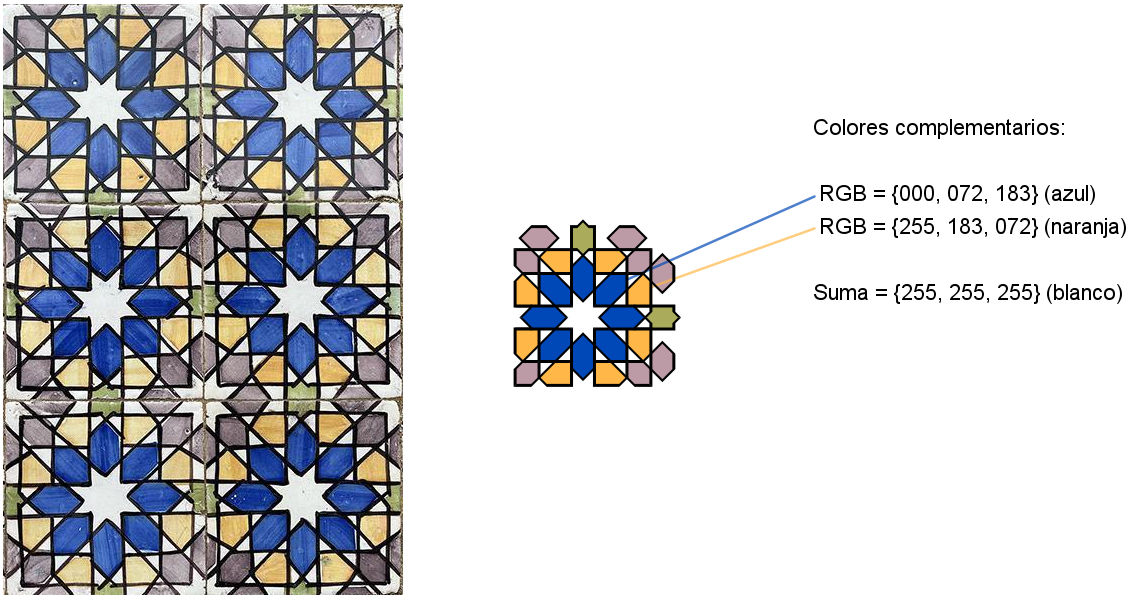
A la izquierda de la imagen puedes ver una foto del mosaico original. A su derecha, la recreación con GeoGebra. Los colores de los polígonos centrales son complementarios, lo que realza el contraste, aumentando la sensación luminosa en el espectador.[br][br]Observa que no es un azulejo sencillo, sino compuesto de varios y diferentes polígonos. Además, los trazos negros, remarcando sus bordes, dificulta todavía más su tratamiento, como [url=https://www.geogebra.org/m/fwpemasd#material/yjvfqgjp]he descrito[/url] en [i]La fábrica de teselados[/i]. Para evitarlo, he recreado los trazos como finos rectángulos coloreados en negro. [br][br]Este libro contiene las que, seguramente, son las primeras teselaciones "completas" en el disco de Poincaré realizadas con GeoGebra y, muy probablemente, este es el primer mosaico hiperbólico realizado con un azulejo portugués. Ahora bien, para realizar [b]cualquier otro[/b] similar basta con cambiar el contenido de las listas que definen el azulejo central, sus reflexiones sucesivas se efectuarán automáticamente.

[color=#999999]Autor de la actividad: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]