Teselaciones regulares
En este libro GeoGebra se exponen procedimientos para crear teselaciones regulares a partir de un azulejo principal, consumiendo un mínimo de recursos. Estas teselaciones no se limitan a las habituales tres de la geometría euclídea, sino que abarcan también las cinco de la geometría elíptica y las infinitas de la hiperbólica. Para lograrlo, se recurre al uso del rastro activado. Gran parte de lo expuesto en este libro formó parte de la conferencia [i]GeoGebra, el explorador matemático[/i] ([url]https://geogebra.es/coimbra/[/url]) presentada por el autor en el II Congreso Internacional de GeoGebra ([url]https://congresogeogebra.org/[/url]), celebrado en Coímbra del 23 al 25 de octubre de 2025. Rafael Losada Liste Instituto GeoGebra de Cantabria
Tabla de Contenidos
- Introducción
- Introducción
- Teselaciones regulares
- Grafos, dualidad y número cromático
- Geometría euclídea
- Teselaciones regulares euclideas
- Geometría elíptica
- Teselación {3, 3}. Tetraedro
- Teselación {3, 4}. Octaedro
- Teselación {3, 5}. Icosaedro
- Teselación {4, 3}. Cubo
- Teselación {5, 3}. Dodecaedro
- Geometría hiperbólica
- Teselación {4, 6}
- Cíclido de Dupin (inversión de un toro) y cadena de Steiner
- Cadenas de Steiner
- Teselación {6, 4}
- Teselación de Coxeter
- Escher, Circle Limit I
- Teselación {5, 5}
- Autodualidad
- Teselación hiperbólica {p, q}
- Un mismo mosaico en las tres geometrías
- Rastro de imagen
- Mosaico euclídeo
- Mosaico elíptico
- Mosaico hiperbólico
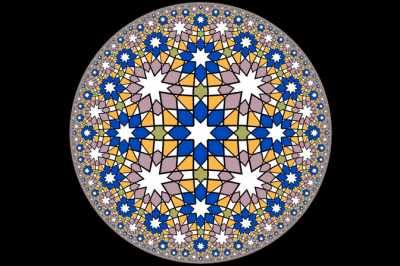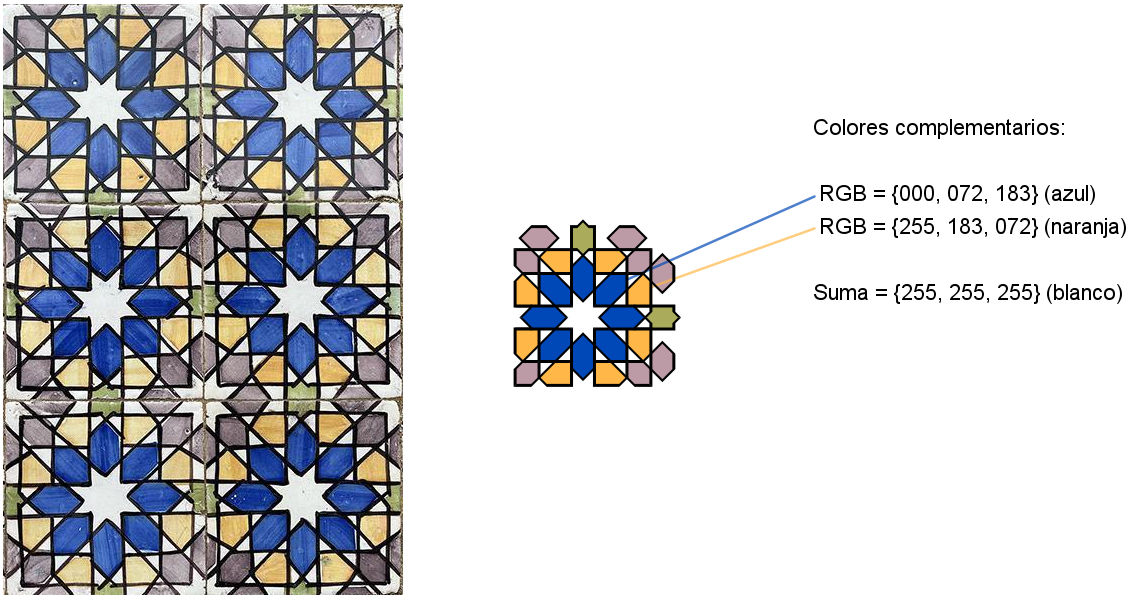
Introducción
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra [/i][url=https://www.geogebra.org/m/vuuufnr8]Teselados regulares euclídeos, elípticos e hiperbólicos[/url].[/color][br][br]Una de las ideas más atractivas para la mente humana es la idea de la supresión de barreras, de límites. La infinitud. La eternidad. El arte islámico supo aprovechar las "teóricamente" infinitas copias de un mismo motivo geométrico para recrear esa idea en quienes transiten entre sus mosaicos.[br][br]Este libro de GeoGebra pretende crear una fábrica de [b]teselaciones regulares[/b]. Es una continuación de [url=https://www.geogebra.org/m/fwpemasd]La fábrica de teselados[/url], pero por un lado restringida a los azulejos que son polígonos regulares y por otro lado ampliada, siguiendo los pasos del genial artista [url=https://es.wikipedia.org/wiki/M._C._Escher]M.C. Escher[/url], a las geometrías elíptica e hiperbólica. [br][br]Las actividades aquí recogidas pueden servir como base para la [b]propuesta de proyectos educativos[/b], ya que permite observar, explorar, conjeturar, comprobar e investigar una amplia gama de situaciones matemáticas, al tiempo que estimula el sentido estético. La exploración de geometrías diferentes a la euclídea permite apreciar sus diferencias y semejanzas.[br][br]Para la exploración de la geometría elíptica elegiremos el más sencillo de los modelos: la esfera. Para la geometría hiperbólica hemos elegido, tanto por su aspecto estético como por ser "abarcable" con la vista, el modelo del disco de Poincaré.[br][br]Consideraremos también el aspecto topológico, en forma de grafo dual asociado a cada teselación. Si no estás familiarizado con ellos, puedes ver una introducción en mi libro de GeoGebra [url=https://www.geogebra.org/m/yybrap57]Redes y Grafos[/url].[br][br]Además de recoger los distintos teselados regulares que se pueden generar, en este libro de GeoGebra he escogido el siguiente mosaico cuadrado del Palacio Nacional de Sintra (Portugal) para ser representado en las tres geometrías: euclídea, elíptica e hiperbólica.
A la izquierda de la imagen puedes ver una foto del mosaico original. A su derecha, la recreación con GeoGebra. Los colores de los polígonos centrales son complementarios, lo que realza el contraste, aumentando la sensación luminosa en el espectador.[br][br]Observa que no es un azulejo sencillo, sino compuesto de varios y diferentes polígonos. Además, los trazos negros, remarcando sus bordes, dificulta todavía más su tratamiento, como [url=https://www.geogebra.org/m/fwpemasd#material/yjvfqgjp]he descrito[/url] en [i]La fábrica de teselados[/i]. Para evitarlo, he recreado los trazos como finos rectángulos coloreados en negro. [br][br]Este libro contiene las que, seguramente, son las primeras teselaciones "completas" en el disco de Poincaré realizadas con GeoGebra y, muy probablemente, este es el primer mosaico hiperbólico realizado con un azulejo portugués. Ahora bien, para realizar [b]cualquier otro[/b] similar basta con cambiar el contenido de las listas que definen el azulejo central, sus reflexiones sucesivas se efectuarán automáticamente.
[color=#999999]Autor de la actividad: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Teselaciones regulares euclideas
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra [/i][url=https://www.geogebra.org/m/vuuufnr8]Teselados regulares euclídeos, elípticos e hiperbólicos[/url].[/color][br][br]En el libro de GeoGebra [url=https://www.geogebra.org/m/fwpemasd#chapter/1168082]La fábrica de teselados[/url] se detallan, entre otras teselaciones, las tres únicas regulares en el plano euclídeo: [br][list][*]{3, 6} formada por triángulos equiláteros (p=3) donde q=6 concurren en cada vértice,[/*][*]{4, 4} formada por cuadrados (p=4) donde q=4 concurren en cada vértice, y[/*][*]{6, 3} formada por hexágonos regulares (p=6) donde q=3 concurren en cada vértice,[/*][/list]Ahora bien, el procedimiento que allí se usa para visualizar las teselaciones es la copia por traslación, siguiendo el orden de la espiral de Ulam. Lamentablemente, este procedimiento no sirve para otras geometrías no euclídeas.[br][br]Por ello, hemos de cambiar el método. En esta construcción, las teselas no se crean trasladando la original a distintas zonas del plano, sino que se crean por reflexión. Es decir, la tesela fundamental se refleja en uno de sus lados, la nueva tesela se vuelve a reflejar en uno de sus lados, etc. [br][br]El proceso sigue realizándose en espiral. En cada paso, la celda de partida (1) [b]se refleja en la recta que contiene a un lado[/b], y la celda obtenida (2) se vuelve a reflejar en el lado que comparte vértice con la celda de partida (1), obteniendo la celda (3), que se vuelve a reflejar... Así hasta que hayan dejado su rastro [b]las q celdas que concurren en ese vértice[/b]. Entonces, se pasa al siguiente vértice no completado y se vuelve a repetir el proceso.[br][br]Atiende a que {3, 6} y {6, 3} son duales, mientras que {4, 4} es autodual. Si [i]q[/i] es par (triángulos y cuadrados), la simetría resultante provoca que los lados de cada polígono descansan todos sobre el mismo conjunto de rectas y el número cromático es 2. Si [i]q[/i] es impar (hexágonos), se rompe esa simetría, de modo que las líneas que unen los lados ya no son rectas, sino quebradas, y el número cromático es 3.[br][br]Observa que el orden seguido, en el plano euclídeo, es exactamente el mismo que el empleado en [url=https://www.geogebra.org/m/fwpemasd#chapter/1168082]La fábrica de teselados[/url] siguiendo la espiral de Ulam. La ventaja, es que este método es fácilmente transportable a la geometría elíptica, sustituyendo "se refleja en la [b]recta [/b]que contiene a un lado" por "se refleja en el [b]plano [/b]que pasa por el origen y contiene a un lado". Y también a la geometría hiperbólica, sustituyendo "se refleja en la recta que contiene a un lado" por "se refleja en la [b]circunferencia [/b]que contiene a un lado".[br][br]Si observas que la ejecución se ralentiza y tienes instalado GeoGebra, puedes acelerar el proceso descargando el [url=https://www.geogebra.org/material/download/format/file/id/wc8hnqq6]archivo GGB[/url].
[color=#999999]Autor de la actividad y [color=#999999]construcciones [/color]GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Teselación {3, 3}. Tetraedro
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra [/i][url=https://www.geogebra.org/m/vuuufnr8]Teselados regulares euclídeos, elípticos e hiperbólicos[/url].[/color][br][br]Esta teselación divide la esfera en cuatro regiones iguales. Cada región es triangular, y en cada vértice coinciden 3 regiones. Su número cromático es 4, es decir, se necesitan 4 colores para pintar el teselado sin que dos regiones vecinas compartan el mismo color. Es una teselación autodual (su dual es ella misma: si unimos con arcos los centros de sus regiones, obtenemos la misma teselación, solo que desplazada).[br][br]Para construirla con GeoGebra, creamos primero el tetraedro regular. Después, proyectamos sobre la esfera, desde su centro, los vértices y puntos medios de las aristas del tetraedro. Solo queda unir los puntos proyectados mediante arcos de circunferencia con el comando ArcoTresPuntos.[br][br]Para colorear las regiones, tenemos tres posibilidades:[list][*]Crear todas las superficies correspondientes.[/*][*]Crear una superficie que vaya dejando su rastro.[/*][*]Crear diversos arcos que vayan dejando su rastro.[/*][/list]La primera opción es la mejor y más sencilla si las superficies son muy pocas, pues se consumen muchos recursos al crearlas. Aquí optaremos por la segunda opción. En el mosaico optaremos por la tercera, pues deberemos colorear muchas superficies.[br][br]Primero, convertimos una arista del tetraedro en una curva paramétrica, y creamos la superficie que une el tercer vértice de la cara con esa arista. Por ejemplo, si una cara del tetraedro es ABC:[center]c = Curva(A + t (B - A), t, 0, 1)[br]s = Superficie((r; arg(k c(t) + (1 - k) C); alt(k c(t) + (1 - k) C)), k, 0, 1, t, 0, 1)[br][/center]Después, trasladamos los vértices A, B y C por las demás caras, mientras la superficie deja su rastro, variando el color a nuestro gusto.[br][br]Si observas que la ejecución se ralentiza y tienes instalado GeoGebra, puedes acelerar el proceso descargando el [url=https://www.geogebra.org/material/download/format/file/id/mqh4nwzp]archivo GGB[/url].
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Teselación {4, 6}
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra [/i][url=https://www.geogebra.org/m/vuuufnr8]Teselados regulares euclídeos, elípticos e hiperbólicos[/url].[/color][br][br]Hemos elegido el disco de Poincaré (que toma como base el círculo unidad) como modelo de representación de la geometría hiperbólica. Las rectas euclídeas ahora son arcos de circunferencias ortogonales a la circunferencia unidad (es decir, de radio 1 y centrada en el origen). [Las circunferencias ortogonales son aquellas que se cortan en puntos cuyas respectivas rectas tangentes son perpendiculares.][br][br]El borde de este círculo representa los puntos infinitamente distantes del centro (y entre sí). La medida de cada distancia se hace mayor a medida que nos aproximamos a ese borde (por eso, visualmente, los arcos empequeñecen).[br][br]En este caso, la teselación está compuesta de cuadrados (hiperbólicos). Todos del mismo tamaño (aunque, insistimos, parezcan empequeñecer al alejarse del centro del disco). Observa cómo los lados de cada cuadrado adoptan la curvatura de los arcos (pues ahora son las "rectas" de esta geometría).[br][br]En cada vértice, concurren 6 cuadrados, pero podrían concurrir todos los que quieras (a partir de 5). Como 6 es un número par, bastan dos colores para colorear todo el teselado.[br][br]El cuadrado central se refleja (por inversión) en las circunferencias que determinan cada uno de sus lados. Los cuadrados obtenidos, vuelven a reflejarse... Así hasta el infinito (borde del círculo unidad, pero en la práctica el proceso seguirá mientras GeoGebra distinga unos vértices de otros; si no quieres esperar, puedes activar la casilla "Imagen final" para observar el resultado después de varios minutos).[br][br]El proceso se realiza en espiral. En cada paso, el cuadrado de partida (1) se refleja en uno de sus lados, y el cuadrado obtenido (2) se vuelve a reflejar en un lado que comparte vértice con el cuadrado (1), obteniendo el cuadrado (3), que se vuelve a reflejar... Así hasta que hayan dejado su rastro [b]los 6 cuadrados que concurren en ese vértice[/b]. Entonces, se pasa al siguiente vértice no completado y se vuelve a repetir el proceso.[br][br]Si observas que la ejecución se ralentiza y tienes instalado GeoGebra, puedes acelerar el proceso descargando el [url=https://www.geogebra.org/material/download/format/file/id/vnqren38]archivo GGB[/url].
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]
Rastro de imagen
[color=#999999]Esta actividad pertenece al [i]libro de GeoGebra [/i][url=https://www.geogebra.org/m/vuuufnr8]Teselados regulares euclídeos, elípticos e hiperbólicos[/url].[/color][br][br]Tal como se detalla en [url=https://www.geogebra.org/m/fwpemasd#material/sdhau7za]La fábrica de teselados[/url], el modo más sencillo de reproducir una imagen por toda la pantalla es usarla como relleno de una figura plana, como por ejemplo un círculo. Ten en cuenta que la imagen siempre es rectangular (o cuadrada). [br][br]Es casi mágico: ¡nuestra "construcción" se reduce a crear un círculo! En la construcción, hemos importado en realidad varias imágenes, todas del mismo azulejo pero con tamaño diferente. Esto permite que, al mover un deslizador, se genere un aparente efecto zum, obteniendo una visión más amplia del mosaico.[br][br]Para observarlo, activa la casilla "Imagen como Rastro". Después, [b]haz zum con la rueda del ratón sobre el círculo[/b]. Cuando este cubra toda la pantalla, usa el deslizador.[br][br]Ahora bien, lamentablemente, este simple procedimiento solo es válido para azulejos rectangulares en el plano euclídeo.
[color=#999999]Autor de la actividad y construcción GeoGebra: [url=https://www.geogebra.org/u/rafael]Rafael Losada[/url].[/color]