Equations of branches of implicitly defined curves

Roman Chijner, Apr 25, 2025

[b]Statement of the problem:[/b] The curve is given in implicit form as g(x, y) = 0, for example a circle as y² + x² = 1. [b]Find[/b]: the explicit form of the equations y=f(x) for each of the k branches of the curve, i.e. {fᵢ(x)}, where i=1..k. For a circle, for example, f₁(x) = sqrt(1-x²) for y > 0, and f₂(x) = − sqrt(1-x²) for y < 0. If f(x, y) is a quadratic function with respect to variable y, GeoGebra can easily find the roots in symbolic form, y₁(x) and y₂(x). For polynomials of the 3rd and 4th degree, knowing the existing rigorous [url]https://www.geogebra.org/m/v4fvf8nx[/url] of their equations in symbolic form, one can find the equations of the branches {fᵢ(x)} of the corresponding plane curves using complex functions.

Table of Contents

  1. Multifocal plane curves
    1. Ellipses and Hyperbolas defined geometrically as locus of points
    2. Cassini ovals and their orthogonal trajectories (hyperbolas)
    3. What is the Locus of a point that moves in such a way that it's sum of the squares of the distance (with weight factors) to N fixed points remains constant?
    4. Construction of multifocus curves, whose locus is relative to |x - xᵢ| - distances of some selected points - foci, having the given conservation properties of some selected value
    5. 1. Images of the construction of multifocal curves corresponding to the potential lines of the electrostatic field
    6. 2. Images of the construction of multifocal curves corresponding to "potential lines"-Contour lines for various "charge" configurations of n-ellipse/hyperbola
    7. 3. Images of the construction of multifocal curves corresponding to "potential lines"-Contour lines for various "charge" configurations of n-Lemniscate
  2. Biquadratic equation
    1. Finding explicit expressions of four real functions for an implicitly defined plane curve (Trifolium curve) whose equation is biquadratic in the variable y
    2. Branches of an implicitly defined biquadratic curve found using complex functions: Trifolium curve
    3. Branches of an implicitly defined biquadratic curve found using complex functions: Cartesian oval
    4. Images: Branches of an implicitly defined biquadratic curve found using complex functions: Cartesian oval
  3. Examples of finding the equations of branches of implicitly defined cubic curves
    1. An example of finding explicit equations for curves using complex functions that make up an implicitly defined cubic curve
    2. Images: An example of finding explicit equations for curves using complex functions that make up an implicitly defined cubic curve
  4. Examples of an implicit equation of a plane curve of the quartic equations
    1. An example of finding explicit equations for curves using exact roots as complex functions that make up an implicitly defined quartic plane curve whose equation has 15 coefficients
    2. Images. An example of finding explicit equations for curves using exact roots as complex functions that make up an implicitly defined quartic plane curve whose equation has 15 coefficients

1.

Multifocal plane curves

  • 1. Ellipses and Hyperbolas defined geometrically as locus of points
  • 2. Cassini ovals and their orthogonal trajectories (hyperbolas)
  • 3. What is the Locus of a point that moves in such a way that it's sum of the squares of the distance (with weight factors) to N fixed points remains constant?
  • 4. Construction of multifocus curves, whose locus is relative to |x - xᵢ| - distances of some selected points - foci, having the given conservation properties of some selected value
  • 5. 1. Images of the construction of multifocal curves corresponding to the potential lines of the electrostatic field
  • 6. 2. Images of the construction of multifocal curves corresponding to "potential lines"-Contour lines for various "charge" configurations of n-ellipse/hyperbola
  • 7. 3. Images of the construction of multifocal curves corresponding to "potential lines"-Contour lines for various "charge" configurations of n-Lemniscate

1.1.

Ellipses and Hyperbolas defined geometrically as locus of points

Inspired by material from Wikipedia: [url=https://en.wikipedia.org/wiki/Ellipse#Definition_as_locus_of_points]Ellipse[/url] and [url=https://en.wikipedia.org/wiki/Hyperbola#As_locus_of_points]Hyperbola[/url] as locus of points. [br]
– Roman Chijner

1.2.

–

1.3.

–

1.4.

–

1.5.

–

1.6.

–

1.7.

–

2.

Biquadratic equation

  • 1. Finding explicit expressions of four real functions for an implicitly defined plane curve (Trifolium curve) whose equation is biquadratic in the variable y
  • 2. Branches of an implicitly defined biquadratic curve found using complex functions: Trifolium curve
  • 3. Branches of an implicitly defined biquadratic curve found using complex functions: Cartesian oval
  • 4. Images: Branches of an implicitly defined biquadratic curve found using complex functions: Cartesian oval

2.1.

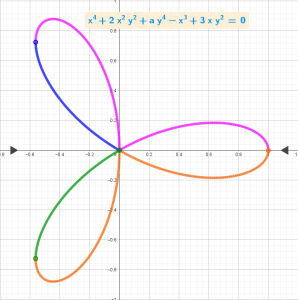
Finding explicit expressions of four real functions for an implicitly defined plane curve (Trifolium curve) whose equation is biquadratic in the variable y

[size=85]x⁴ + 2x² [b]y²[/b] + a [b]y[/b]⁴ - x³ + 3x [b]y²[/b] = 0 [br] Biquadratic equation, the solution [b]y[/b]=y([b]x[/b]) of which is found by the formulas[url=https://eqworld.ipmnet.ru/en/solutions/ae/ae0104.pdf] EqWorld[/url]. The branches of the implicit function generally correspond to the real functions f(x) on the considered domains of definition of the implicit function.[br] The vertical asymptotes are found using the [url=https://en.wikipedia.org/wiki/Implicit_function_theorem]implicit function theorem[/url] and the calculations are done in CAS.[br] *Following [url=https://www.geogebra.org/m/kwdbdznt]applet[/url]: Branches of an implicitly defined biquadratic curve found using complex functions.[/size]
– Roman Chijner

2.2.

–

2.3.

–

2.4.

–

3.

Examples of finding the equations of branches of implicitly defined cubic curves

  • 1. An example of finding explicit equations for curves using complex functions that make up an implicitly defined cubic curve
  • 2. Images: An example of finding explicit equations for curves using complex functions that make up an implicitly defined cubic curve

3.1.

An example of finding explicit equations for curves using complex functions that make up an implicitly defined cubic curve

[size=85][u][b]Statement of the problem:[/b][/u][br]The curve is given in [b]implicit[/b] form as g(x, y) = 0, for example a circle as y² + x² = 1.[br][u][b] Find:[/b][/u][br]the [b]explicit [/b]form of the equations y=f(x) for each of the [b]k[/b] branches of the curve, i.e. {f[b]ᵢ[/b](x)}, where i=1..k. For a circle, for example, f₁(x) = sqrt(1-x²) for y > 0, and f₂(x) = − sqrt(1-x²) for y < 0. If f(x, y) is a quadratic function with respect to variable [b]y[/b], GeoGebra can easily find the [b]roots [/b]in symbolic form, y₁(x) and y₂(x).[br] For polynomials of the 3rd and 4th degree, knowing the existing rigorous [url=https://www.geogebra.org/m/v4fvf8nx][u][b]solutions[/b][/u][/url] of their equations in symbolic form, one can find the equations of the branches {f[b]ᵢ[/b](x)} of the corresponding plane curves using complex functions.[br] Earlier, I considered biquadratic equations for the [url=https://www.geogebra.org/m/kwdbdznt][u][b]Trifolium curve[/b][/u][/url] and the [url=https://www.geogebra.org/m/cgfbcxau][u][b]Cartesian oval[/b][/u][/url]. These examples illustrate the application of complex functions. In these cases, it is possible to find the equations of the branches of curves using both [i][b]real functions[/b][/i] and [i][b]complex functions[/b][/i], from the real part of the functions of which only those sections are left where the corresponding complex part is missing, i.e. Im(x)=0.[br][/size][size=85] This applet considers an example from mathstackexchange: [url=https://math.stackexchange.com/questions/3980344/branches-of-implicitly-defined-cubic-curves]Branches of implicitly defined cubic curves[/url] for an implicitly defined cubic curve [b]a y³ + b y² + c y + d(x) = 0 where d(x)=-5 x³ + x² + 45x - c0[/b], for which I found explicit equations of the curves of its branches using complex functions.[br] Images of three examples are in the [url=https://www.geogebra.org/m/rek5mz4n]applet.[/url][/size]
– Roman Chijner

3.2.

–

4.

Examples of an implicit equation of a plane curve of the quartic equations

  • 1. An example of finding explicit equations for curves using exact roots as complex functions that make up an implicitly defined quartic plane curve whose equation has 15 coefficients
  • 2. Images. An example of finding explicit equations for curves using exact roots as complex functions that make up an implicitly defined quartic plane curve whose equation has 15 coefficients

4.1.

An example of finding explicit equations for curves using exact roots as complex functions that make up an implicitly defined quartic plane curve whose equation has 15 coefficients

[size=85] This applet illustrates an example of finding equations of branches of a plane curve of degree four (specified implicitly) using existing[b][url=https://www.geogebra.org/m/v4fvf8nx] rigorous solutions[/url][/b] in the form of complex functions in symbolic form.[br] The [b] [url=https://en.wikipedia.org/wiki/Quartic_plane_curve]Quartic plane curve[/url] [/b]of the [b]fourth order [/b]has 15 coefficients: A [b]x[/b][sup][b]4[/b][/sup]+B [b]y[sup]4[/sup][/b]+C [b]x[sup]3 [/sup]y[/b]+D [b]x[sup]2 [/sup]y[sup]2[/sup][/b]+E [b]x y[sup]3[/sup][/b]+F [b]x[sup]3[/sup][/b]+G [b]y[sup]3[/sup][/b]+H [b]x[sup]2 [/sup]y[/b]+I [b]x y[sup]2[/sup][/b]+J [b]x[sup]2[/sup][/b]+K [b]y[sup]2[/sup][/b]+L[b] x y[/b]+M[b] x[/b]+N [b]y[/b]+P=0, where at least one of A, B, C, D and E is non-zero. You can explore these curves by adjusting the coefficients using the sliders.[br] Images of three examples are presented in the [url=https://www.geogebra.org/m/wmwsrksg]applet[/url][b].[/b][br][/size]
– Roman Chijner

4.2.

–

Information