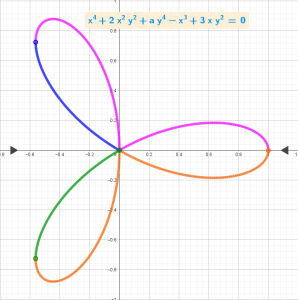
[b]Statement of the problem:[/b]
The curve is given in implicit form as g(x, y) = 0, for example a circle as y² + x² = 1.
[b]Find[/b]:
the explicit form of the equations y=f(x) for each of the k branches of the curve, i.e. {fᵢ(x)}, where i=1..k. For a circle, for example, f₁(x) = sqrt(1-x²) for y > 0, and f₂(x) = − sqrt(1-x²) for y < 0. If f(x, y) is a quadratic function with respect to variable y, GeoGebra can easily find the roots in symbolic form, y₁(x) and y₂(x).
For polynomials of the 3rd and 4th degree, knowing the existing rigorous [url]https://www.geogebra.org/m/v4fvf8nx[/url] of their equations in symbolic form, one can find the equations of the branches {fᵢ(x)} of the corresponding plane curves using complex functions.