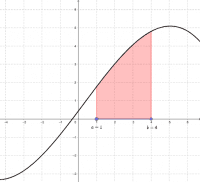
Permite cambiar :
A definición función (f(x))
Os extremos do intervalo [a,b], arrastrandoos na vista gráfica, ou introducindo as súas coordenadas para maior precisión.
O número de subintervalos da partición (n).
A FUNCIÓN f(X) DEBE SER CONTINUA NO INTERVALO [a, b], XA QUE SE NON , O PROGRAMA PODE PRESENTAR ERROS
A partir dos datos anteriores:
Seleccionando "Datos da Partición" proporciona : os extremos de cada subintervalo da partición (Xi), a amplitude de cada subintervalo (Xi+1-Xi), o máximo de f(x) en cada subintervalo (Mi), o mínimo de f en cada subintervalo (mi), a área de cada rectángulo de "altura máxima" e base a amplitude dun subintervalo (Xi+1-Xi)Mi, e finalmente a área de cada rectángulo de "altura mínima" e base a amplitude dun subintervalo, (Xi+1-Xi)mi
Seleccionando "Suma Superior" proporciona o valor númérico e a representación gráfica, da Suma Superior da función f(x) correspondente a partición de tamaño n dun intervalo [a,b]
Seleccionando "Integral Definida" proporciona o valor numérico e a representación gráfica da integral definida de f(x) en [a,b].
POSIBLES PREGUNTAS:
1) Que sucede a medida que aumenta o número de intervalos da partición (n), entre a suma superior, a suma inferior e o valor da integral definida ?
2) Que signo pode tomar a integral definida?
3) Cuando coincide área baixo a curva e integral definida?